 |
A B. 4673. feladat (2014. december) |
B. 4673. Az \(\displaystyle ABCD\) húrnégyszög átlóinak metszéspontja \(\displaystyle E\), körülírt körének középpontja \(\displaystyle K\). Az \(\displaystyle AB\) és \(\displaystyle CD\) oldalegyenesek metszéspontja \(\displaystyle F\), a \(\displaystyle BC\) és \(\displaystyle DA\) oldalegyenesek metszéspontja \(\displaystyle G\). A \(\displaystyle BFC\) és \(\displaystyle CGD\) háromszögek körülírt köreinek második metszéspontja \(\displaystyle H\). Igazoljuk, hogy a \(\displaystyle K\), \(\displaystyle E\) és \(\displaystyle H\) pontok egy egyenesen fekszenek.
Javasolta: Miklós Szilárd (Herceghalom)
(4 pont)
A beküldési határidő 2015. január 12-én LEJÁRT.
Megoldási ötlet: Keressünk egyenlő szögeket.
Megoldás. Először azt látjuk be, hogy a \(\displaystyle G\), \(\displaystyle H\), \(\displaystyle F\) pontok egy egyenesbe esnek.
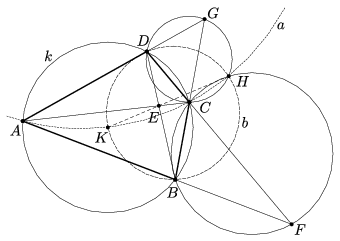
\(\displaystyle FHCB\) húrnégyszög, mivel mindegyik pontja rajta van a \(\displaystyle BFC\) háromszög köré írt körén. Hasonlóan \(\displaystyle HGDC\) is húrnégyszög. Mindebből
\(\displaystyle FHC\sphericalangle =180^\circ-FBC\sphericalangle =CBA\sphericalangle,\)
\(\displaystyle CHG\sphericalangle =180^\circ-GDC\sphericalangle =CDA\sphericalangle.\)
\(\displaystyle CBA\sphericalangle +CDA\sphericalangle =180^\circ\), hiszen \(\displaystyle ABCD\) húrnégyszög. Tehát \(\displaystyle FHC\sphericalangle+CHG\sphericalangle= 180^\circ\), így a \(\displaystyle G\), \(\displaystyle H\), \(\displaystyle F\) pontok valóban egy egyenesbe esnek.
Most belátjuk, hogy a \(\displaystyle HCKA\), illetve a \(\displaystyle HDKB\) négyszögek húrnégyszögek.
Az \(\displaystyle ABCD\) húrnégyszög megváltoztatásával bizonyos szögek megváltozhatnak, de az, hogy a két négyszög húrnégyszög ekkor is analóg módon bizonyítható. (Ilyen eset lehet, ha például a \(\displaystyle K\) pont átkerül az \(\displaystyle AC\) szakasz \(\displaystyle B\)-vel átellenes oldalára.)
Ehhez a \(\displaystyle CKA\sphericalangle +AHC\sphericalangle =180^\circ\), illetve a \(\displaystyle DKB\sphericalangle +BHD\sphericalangle =180^\circ\) feltételeket kell igazolnunk.
A kerületi és középponti szögek tétele miatt:
\(\displaystyle CKA\sphericalangle =2\cdot CBA\sphericalangle =2\beta, \quad\text{valamint}\quad DKB\sphericalangle =2\cdot DAB\sphericalangle =2\alpha. \)
Tehát elegendő belátnunk, hogy:
\(\displaystyle AHC\sphericalangle =180^\circ-2\beta \quad\text{és} \quad BHD\sphericalangle =180^\circ-2\alpha,\)
\(\displaystyle AHC\sphericalangle =180^\circ-(FHC\sphericalangle +AHG\sphericalangle), \quad BHD\sphericalangle =180^\circ-(FHB\sphericalangle +DHG\sphericalangle).\)
Most pedig igazoljuk, hogy:
\(\displaystyle FHB\sphericalangle =DHG\sphericalangle =\alpha, \quad FHC\sphericalangle =AHG\sphericalangle =\beta. \)
\(\displaystyle FHB\sphericalangle =FCB\sphericalangle\) az \(\displaystyle FHCB\) húrnégyszögben, és
\(\displaystyle FCB\sphericalangle =180^\circ-BCD\sphericalangle =DAB\sphericalangle =\alpha. \)
Ugyanígy \(\displaystyle DHG\sphericalangle =DCG\sphericalangle =180^\circ-BCD\sphericalangle =DAB\sphericalangle =\alpha\). A másik szögpárnál szükségünk lesz még egy húrnégyszögre, a \(\displaystyle BHGA\) négyszögre. Ez a négyszög is húrnégyszög, hiszen
\(\displaystyle BHG\sphericalangle =180^\circ-BHF\sphericalangle =180^\circ-BCF\sphericalangle =BCD\sphericalangle =180^\circ-DAB\sphericalangle, \)
és így \(\displaystyle GAB\sphericalangle +BHG\sphericalangle =180^\circ\). Tehát \(\displaystyle GABH\) húrnégyszög, így:
\(\displaystyle AHG\sphericalangle =ABG\sphericalangle =ABC\sphericalangle =\beta. \)
Mivel \(\displaystyle FHCB\) húrnégyszög:
\(\displaystyle CHF\sphericalangle =180^\circ-FBC\sphericalangle =ABC\sphericalangle =\beta. \)
Tehát igazoltuk, hogy a \(\displaystyle HCKA\) és a \(\displaystyle HDKB\) négyszögek húrnégyszögek, így rátérhetünk a bizonyítandó állításra.
Legyen a \(\displaystyle HCKA\) négyszög köré írt köre \(\displaystyle a\), \(\displaystyle HDKB\)-é \(\displaystyle b\), \(\displaystyle ABCD\)-é pedig \(\displaystyle k\). Végezzünk \(\displaystyle k\) alapkörű inverziót (az I. 324. feladat az inverzió bemutatása volt prezentáció segítségével: http://www.komal.hu/verseny/feladat.cgi?a=feladat&f=I324&l=hu), mely során \(\displaystyle a\)-t és \(\displaystyle b\)-t invertáljuk. Mindkét kör képe egyenes lesz, hiszen ezen körök átmennek \(\displaystyle k\) középpontján, \(\displaystyle K\)-n. Másrészről, mivel \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) egyaránt \(\displaystyle k\) pontjai, az inverzió ezeket helyben hagyja. Tehát \(\displaystyle a\) képe egy egyenes, mely átmegy az \(\displaystyle A\) és \(\displaystyle C\) pontokon -- ez éppen az \(\displaystyle AC\) egyenes. Hasonlóan \(\displaystyle b\) képe a \(\displaystyle BD\) egyenes lesz. Ezek metszéspontja \(\displaystyle E\). Az \(\displaystyle a\) és \(\displaystyle b\) invertálása során kaptunk egy olyan pontot, mely \(\displaystyle a\) és \(\displaystyle b\) inverzén is rajta van. Az inverzió két különböző ponthoz két különböző pontot rendel. Ez azt jelenti, hogy \(\displaystyle E\) az \(\displaystyle a\) és \(\displaystyle b\) közös pontjának inverze lesz. Az \(\displaystyle a\) és \(\displaystyle b\) két közös ponttal rendelkezik: \(\displaystyle H\)-val és \(\displaystyle K\)-val. Közülük \(\displaystyle K\) az alapkör középpontja, melynek nincs inverze. Ebből következik, hogy \(\displaystyle H\) inverze \(\displaystyle E\), vagyis \(\displaystyle K\), \(\displaystyle H\) és \(\displaystyle E\) egy egyenesen van.
Németh Balázs (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 9. évf.) dolgozata alapján
Statisztika:
21 dolgozat érkezett. 4 pontot kapott: Gál Boglárka, Geng Máté, Imolay András, Keresztfalvi Bálint, Khayouti Sára, Kocsis Júlia, Nagy-György Pál, Németh 123 Balázs, Szebellédi Márton, Szőke Tamás, Vághy Mihály, Williams Kada. 3 pontot kapott: Gyulai-Nagy Szuzina, Heinc Emília. 2 pontot kapott: 2 versenyző. 0 pontot kapott: 5 versenyző.
A KöMaL 2014. decemberi matematika feladatai

