 Problem B. 4758. (December 2015)
Problem B. 4758. (December 2015)
B. 4758. What is the minimum number of different lines determined by the sides of a (not necessarily convex) 2015-sided polygon?
Proposed by D. Lenger, Budapest
(6 pont)
Deadline expired on January 11, 2016.
Solution. \(\displaystyle k\) lines have at most \(\displaystyle \binom{k}{2}\) intersections so it is necessary that \(\displaystyle \binom{k}{2}\ge2015\). \(\displaystyle \binom{64}{2}=2016\), so we need at least 64 lines.
But, it is not enough. On a line, there are at most 63 intersections, and they are making at most 62 (bounded) segments. But these 62 segments can make at most 31 sides of the 2015-gon, because between every two sides we need a gap. So we have at most \(\displaystyle 64\cdot 31=1984\) sides, which are less than 2015.
So we need at least 65 lines. I will show a way that we can make a 2015-gon from 65 well-chosen lines. First, take a regular 65-gon and choose its sidelines to be the 65 lines. It has a lot of symmetries and we will use that.
Now we will give colours to the segments. A line has 63 segments, colouring it alternately red and blue, starting with red, so the last one will be also red.
Because of the symmetries, every line can be transformed into every other by a rotation and it also keeps the colouring. So the 'furthest' segments are red, the next ones are blue, etc. Here are two figure for 13 lines with the colouring.
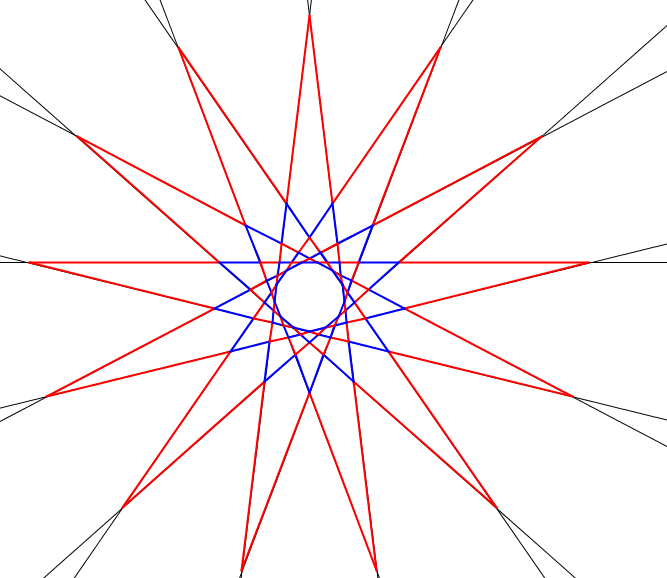
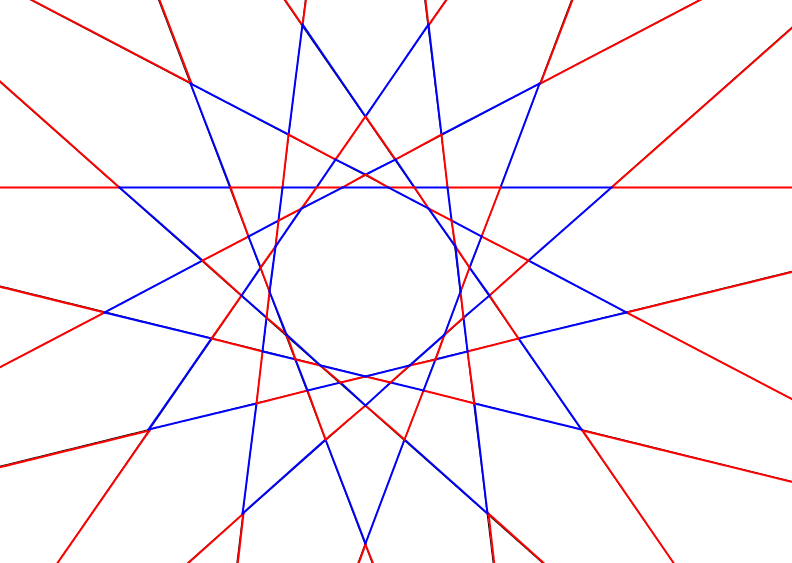
It is also true that the furthest segments form a red \(\displaystyle 130\)-gon (that I will call a 'star'), and the next blue ones also form a star, etc. 63 is odd so after 16 red and 15 blue stars, there remain 65 blue segments, which ones form a blue regular 65-gon, which is our original 65-gon but we won't use this fact. (The figures shows 3 red stars, 2 blue stars and a blue regular 13-gon.)
We have \(\displaystyle 16\cdot 130=2080\) red segments, and we will make our 2015-gon starting with these. These are not connected, we will solve that. I will use the 13 lines figure, but it also works with 65 lines. Choose two adjacent red stars. We can connect them, with the following trick:
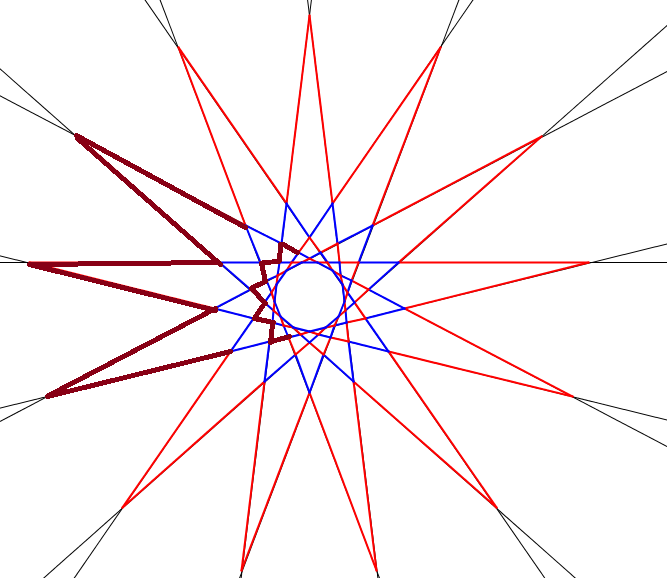
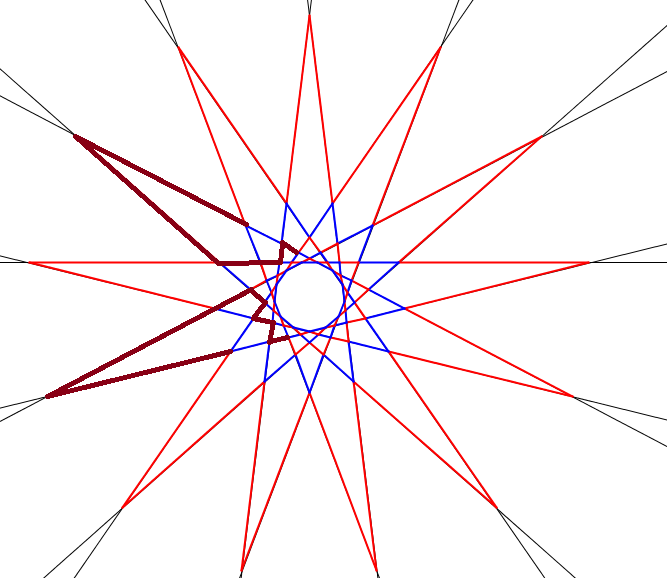
Some segments will became part of the the polygon and some will stop being part of the polygon. The thin red segments on the first figure don't change, and the dark red ones on the first figure change into the dark ones on the second figure (some of them does not change). This trick decreases the total number of red sides by 4. (NOT the number of segments, because some side is made from more than one segments.)
And we can use this trick at every two adjacent red stars, because the segment we used are locally the same, and 65 is big enough, so on a star we can choose the 3+5 dark red 'spike' disjoint.
That means we lose \(\displaystyle 15\cdot4=60\) sides this way, so we have a 2020-gon. We need 5 less side.
We modify the trick a little. We do the same 'down', as 'up':


This one decreases the number of sides by 6. We use it instead of the original only once, so we get 2018 sides.
We will lose the last 3 side, at the middle, with this one:
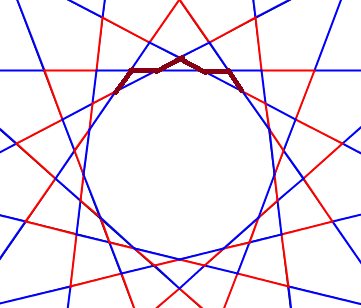
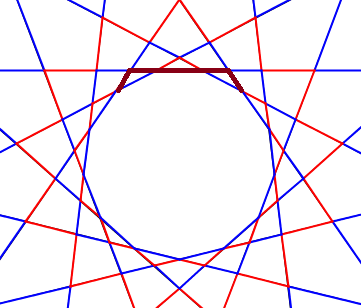
Statistics:
29 students sent a solution. 6 points: Baran Zsuzsanna, Borbényi Márton, Bukva Balázs, Gáspár Attila, Hansel Soma, Imolay András, Kovács 246 Benedek, Váli Benedek. 5 points: Lajkó Kálmán. 2 points: 8 students. 1 point: 4 students. 0 point: 8 students.
Problems in Mathematics of KöMaL, December 2015
