Problem B. 4806. (September 2016)

B. 4806. Given a circular disc \(\displaystyle K\) and two points on it, separated by a distance larger than \(\displaystyle 2\) units. Show that \(\displaystyle K\) contains a disc of unit radius that does not contain either of the two points.

Proposed by Gy. Károlyi, Budajenő

(3 pont)

Deadline expired on October 10, 2016.

Sorry, the solution is available only in Hungarian. Google translation

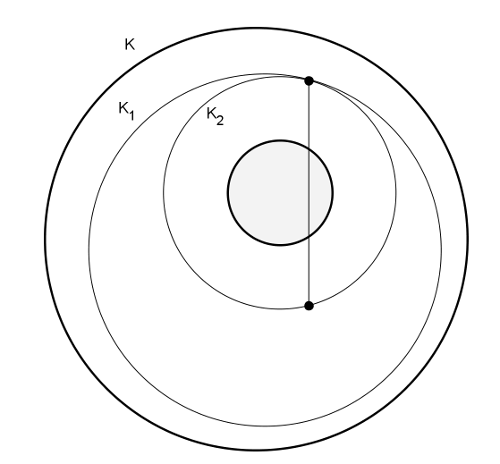
Megoldás. A körlemezt középpontosan kicsinyíthetjük először az egyik pontból úgy, hogy a másik pont a kapott (\(\displaystyle K\)-ban fekvő) \(\displaystyle K_{(1)}\) körlemez kerületére essen. Utána \(\displaystyle K_{(1)}\)-et kicsinyíthetjük ebből a kerületén levő pontból úgy, hogy a kapott — \(\displaystyle K_{(1)}\)-ben fekvő — \(\displaystyle K_{(2)}\) körnek a másik pont is a kerületén legyen. A \(\displaystyle K_{(2)}\) körlemez sugara \(\displaystyle r>1\), mivel benne az adott két pont távolsága 2-nél nagyobb. Így \(\displaystyle K_{(2)}\)-t a középpontjából \(\displaystyle 1/r\) arányban kicsinyítve egy kívánt egységsugarú körlemezhez jutunk.

Statistics:

161 students sent a solution.
3 points:	86 students.
2 points:	29 students.
1 point:	23 students.
0 point:	21 students.
Unfair, not evaluated:	2 solutionss.

Problems in Mathematics of KöMaL, September 2016