Problem B. 4816. (October 2016)

B. 4816. Let \(\displaystyle O\) denote the midpoint of line segment \(\displaystyle AB\), and let \(\displaystyle C\) be the point on line segment \(\displaystyle OB\) for which \(\displaystyle \frac{AO}{OC}=\frac{OC}{CB}\). Point \(\displaystyle D\) is one of the points where the perpendicular drawn at point \(\displaystyle C\) to \(\displaystyle AB\) intersects the Thales circle of \(\displaystyle AB\). Points \(\displaystyle E\) and \(\displaystyle F\) are the two intersections of line \(\displaystyle AD\) with the circle of radius \(\displaystyle OC\) centred at \(\displaystyle O\). Determine the size of the angle \(\displaystyle EOF\).

Proposed by Sz. Miklós, Herceghalom

(3 pont)

Deadline expired on November 10, 2016.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Válasszuk a \(\displaystyle CB\) szakaszt egységnyinek és legyen az \(\displaystyle OC\) szakasz hossza \(\displaystyle q\). Az \(\displaystyle OC\) sugarú kör \(\displaystyle E\) és \(\displaystyle F\) pontjaira szintén \(\displaystyle EO=FO=q\). Az \(\displaystyle AD\) szakasz felezőpontja legyen a \(\displaystyle T\) pont.

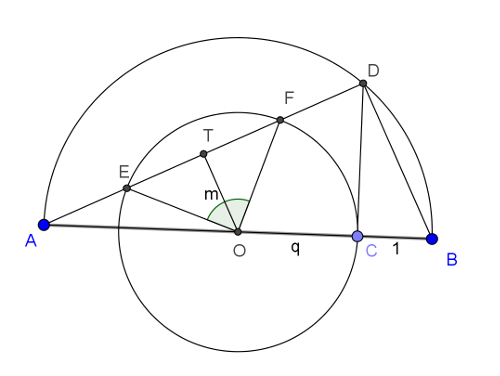
Az \(\displaystyle AO\) szakasz hosszára a feltételben szereplő arányból \(\displaystyle AC=q^{2}\) adódik. Az \(\displaystyle ABD\) derékszögű háromszög átfogója \(\displaystyle AB=2q^{2}\), a \(\displaystyle BD\) befogó merőleges vetülete az átfogón egységnyi, így a befogótétel alapján \(\displaystyle BD=q\sqrt{2}\). Az \(\displaystyle AB\) szakasz felezőpontja \(\displaystyle O\), az \(\displaystyle AD\) szakasz felezőpontja \(\displaystyle T\), így az \(\displaystyle OT\) szakasz is feleakkora, mint a \(\displaystyle BD\), \(\displaystyle OT=q\frac{\sqrt{2}}{2}\). Most tekintsük az \(\displaystyle OTE\) és \(\displaystyle OTF\) derékszögű háromszögeket. A befogó és az átfogó arányából látható, hogy egybevágóak és egyenlő szárúak. Az \(\displaystyle EOF\) szög derékszög.

Statistics:

77 students sent a solution.
3 points:	53 students.
2 points:	10 students.
1 point:	5 students.
0 point:	9 students.

Problems in Mathematics of KöMaL, October 2016