 Problem B. 4820. (October 2016)
Problem B. 4820. (October 2016)
B. 4820. Four lattice points in a lattice of regular triangles of unit side form the vertices of a parallelogram \(\displaystyle \mathcal{P}\). The area of \(\displaystyle \mathcal{P}\) is \(\displaystyle \sqrt{3}\) units. What may be the sum of the lattice segments in the interior of \(\displaystyle \mathcal{P}\)?
(6 pont)
Deadline expired on November 10, 2016.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásvázlat. A megoldás alapja egy, a Pick-tételhez hasonló tény.
Tetszőleges \(\displaystyle \mathcal{R}\) sokszög esetén jelöljük
\(\displaystyle \bullet\) \(\displaystyle T(\mathcal{R})\)-rel azt, hogy \(\displaystyle \mathcal{R}\) területe hányszorosa egy rácsháromszög területének,
\(\displaystyle \bullet\) \(\displaystyle B(\mathcal{R})\)-rel a rácsegyenesek \(\displaystyle \mathcal{R}\) belsejébe eső szakaszainak összegét,
\(\displaystyle \bullet\) \(\displaystyle K(\mathcal{R})\)-rel a rácsegyenesek \(\displaystyle \mathcal{R}\) kerületén haladó szakaszainak összegét, végül legyen
\(\displaystyle \bullet\) \(\displaystyle S(\mathcal{R})=2B(\mathcal{R})+K(\mathcal{R})\).
Lemma. Tetszőleges \(\displaystyle \mathcal{R}\) rácssokszög esetén
\(\displaystyle S(\mathcal{R}) = 2B(\mathcal{R})+K(\mathcal{R}) = 3\cdot T(\mathcal{R}). \tag{1} \)
Bizonyítás. Először azt mutatjuk, meg, hogy az \(\displaystyle S\) függvény additív: ha egy \(\displaystyle \mathcal{R}\) sokszöget egyenes szakaszokkal néhány részre, az \(\displaystyle \mathcal{R}_1,\mathcal{R}_2,\ldots,\mathcal{R}_k\) sokszögekre bontunk, akkor
\(\displaystyle S(\mathcal{R})=S(\mathcal{R}_1)+S(\mathcal{R}_2)+\ldots+S(\mathcal{R}_k), \tag{2a} \)
azaz
\(\displaystyle 2B(\mathcal{R})+K(\mathcal{R}) = 2B(\mathcal{R}_1)+K(\mathcal{R}_1)+ 2B(\mathcal{R}_2)+K(\mathcal{R}_2) +\ldots+ 2B(\mathcal{R}_k)+K(\mathcal{R}_k). \tag{2b} \)
Az \(\displaystyle \mathcal{R}_1,\ldots,\mathcal{R}_k\) sokszögek belsejében vagy határán haladó rácsszakaszokat három csoportba oszthatjuk:
\(\displaystyle \bullet\) azok a szakaszok, amelyek valameyik \(\displaystyle \mathcal{R}_i\) belsejébe esnek (az ábrán a piros szakaszok): az ilyenek \(\displaystyle \mathcal{R}\)-nek is belső szakaszai, így ezeket (1b) baloldalán a \(\displaystyle 2B(\mathcal{R})\), a jobboldalon a \(\displaystyle 2B(\mathcal{R}_i)\) tagban számoltuk össze;
\(\displaystyle \bullet\) azok a szakaszok, amelyek egyetlen \(\displaystyle \mathcal{R}_i\) határán haladnak (zöld szakaszok): az ilyenek \(\displaystyle \mathcal{R}\)-nek is határszakaszai, így ezeket (1b) baloldalán a \(\displaystyle K(\mathcal{R})\), a jobboldalon a \(\displaystyle K(\mathcal{R}_i)\) tagban számoltuk össze;
\(\displaystyle \bullet\) azok a szakaszok, amelyek két szomszédos rész, \(\displaystyle \mathcal{R}_i\) és \(\displaystyle \mathcal{R}_j\) határán haladnak (kék szakaszok): az ilyenek \(\displaystyle \mathcal{R}\)-nek belső szakaszai, így ezeket (1b) baloldalán a \(\displaystyle 2B(\mathcal{R})\), a jobboldalon a \(\displaystyle K(\mathcal{R}_i)\) és \(\displaystyle K(\mathcal{R}_j)\) tagokban számoltuk össze.
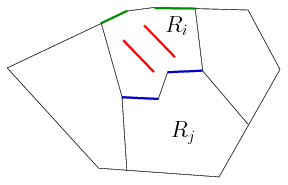
Mindegyik rácsszakaszt ugyanannyiszor számoltuk (2b) két oldalán, így (2b) és vele együtt (2a) is biztosan teljesül.
Az \(\displaystyle S(\mathcal{R})\) függvényhez hasonlóan additív a területettel arányos \(\displaystyle T(\mathcal{R})\) függvény is.
Az (1) képlet igaz az egységnyi rácsháromszögekre; az additivitás miatt igaz
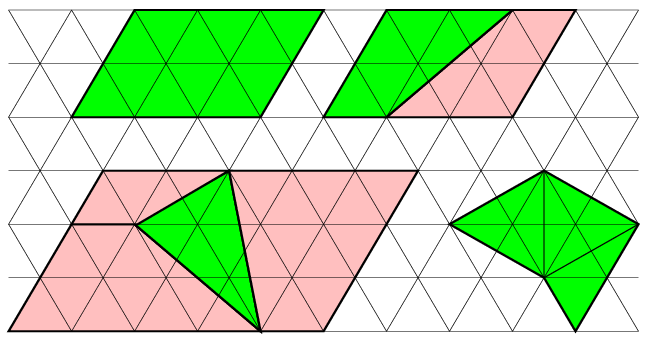
\(\displaystyle \bullet\) minden olyan sokszögre, amely egységnyi rácsháromszögekből összerakható; így például rácsegyenesekkel harárolt paralelogrammákra;
\(\displaystyle \bullet\) minden olyan rácstrapézra, amelynek alapjai és legalább az egyik szára rácsegyenes, ugyanis ezek két egybevágó példányából összerakhatunk egy rácsegyenesekkel határolt paralelogrammát;
\(\displaystyle \bullet\) minden rácsháromszögre, mert ezek előállnak mint egy rácsegyenesekkel határolt paralelogramma és két vagy három trapéz különbsége;
\(\displaystyle \bullet\) minden rácssokszögre, mert a rácssokszögeket néhány átlójukkal rácsháromszögekre bonthatjuk.
A Lemma a feladatban szereplő \(\displaystyle \mathcal{P}\) paralelogrammára is igaz, tehát
\(\displaystyle 2B(\mathcal{P})+K(\mathcal{P}) = 3\cdot T(\mathcal{P}) = 12. \tag{3} \)
A \(\displaystyle B(\mathcal{P})\) helyett egyszerűbb a \(\displaystyle K(\mathcal{P})\) lehetséges értékeit meghatároznunk. A paralelogramma szemközti oldalain ugyannyi, egész számú egységnyi rácsszakasz található, így \(\displaystyle K(\mathcal{P})\) páros egész szám. Ha a valamelyik két szemközti oldal rácsegyenes, akkor a két oldalegyenes távolsága legalább \(\displaystyle \sqrt3/2\), így a két oldal hossza legfeljebb \(\displaystyle 2\) egység. Az nem lehetséges, hogy a paralelogramma mindegyik oldala hossza \(\displaystyle 2\) legyen, mert ilyenkor a paralelogramma már legalább \(\displaystyle 8\) háromszögre bomlik. A \(\displaystyle K(\mathcal{P})\) értéke tehát csak \(\displaystyle 0\), \(\displaystyle 2\), \(\displaystyle 4\) vagy \(\displaystyle 6\) lehet; ezek az értékek lehetségesek is:
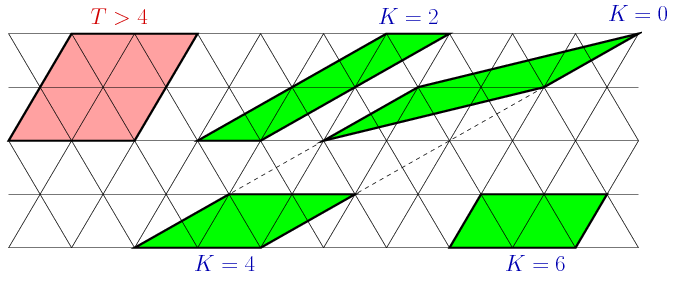
A \(\displaystyle B(\mathcal{P})=\dfrac{12-K(\mathcal{P})}2\) lehetséges értékei tehát \(\displaystyle 6\), \(\displaystyle 5\), \(\displaystyle 4\) és \(\displaystyle 3\).
Statistics:
58 students sent a solution. 6 points: Andó Angelika, Baran Zsuzsanna, Beke Csongor, Borbényi Márton, Deák Bence, Gáspár Attila, Győrffy Ágoston, Imolay András, Kerekes Anna, Kocsis Júlia, Kovács 246 Benedek, Kővári Péter Viktor, Márton Dénes, Matolcsi Dávid, Pap Benedek, Simon Dániel Gábor, Szabó Kristóf, Szakály Marcell, Szemerédi Levente, Tiderenczl Dániel, Tóth Viktor, Vankó Miléna, Várkonyi Dorka, Zólomy Kristóf. 5 points: Daróczi Sándor, Janzer Orsolya Lili. 4 points: 1 student. 3 points: 3 students. 2 points: 12 students. 1 point: 12 students. 0 point: 4 students.
Problems in Mathematics of KöMaL, October 2016
