 Problem B. 4825. (November 2016)
Problem B. 4825. (November 2016)
B. 4825. Problem B. 4825. was already proposed earlier this spring, therefore we replace it with a new problem to be submitted together with the problems in this December issue. We apologize for any inconvenience.
Let us consider the concave hexagon in the figure: the points \(\displaystyle ABCD\) form a unit square, and the triangle \(\displaystyle AEF\) is isosceles, with base length equal to two and one angle equal to \(\displaystyle 135^{\circ}\). By using a single slice, cut the hexagon into two equal pieces. Demonstrate the correctness of your solution.
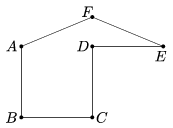
(4 pont)
Deadline expired on January 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásvázlat. Az \(\displaystyle ABC\) derékszögű töröttvonalat forgassuk el \(\displaystyle C\) körül \(\displaystyle 90^{\circ}\)-kal az óramutató járásával megegyező irányban, így épp a \(\displaystyle CDE\) töröttvonalba kerül. Ez adja az ötletet, hogy próbálkozzunk a \(\displaystyle 45^{\circ}\)-os forgatottja mentén vágni. Csak azt kell meggondolni, hogy az \(\displaystyle A\) pont \(\displaystyle 45^{\circ}\)-kal elforgatott képe éppen \(\displaystyle F\), onnan a bizonyítás triviális.
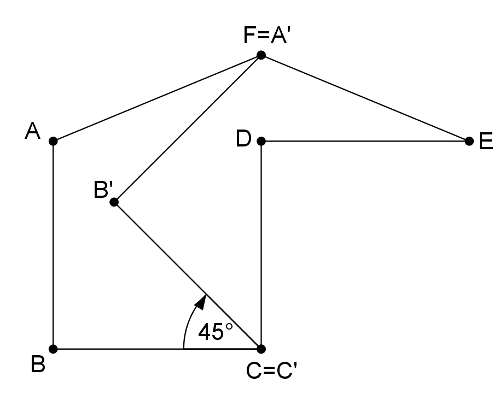
Megjegyzés. Sokan elkövették azt a hibát, hogy nem bizonyították a felbontáskor kapott két ötszög egybevágóságának pontos feltételét. Sokan csak azt látták be, hogy a megfelelő szögek megegyeznek, és hogy egy oldalpár azonos hosszú – arra hivatkozva, hogy a szögek egyezősége miatt az alakzatok hasonlóak, és az azonos oldal miatt egybevágóak is. Ez az állítás háromszögeknél igaz, de nagyobb oldalszámú síkidomokra nem. (Könnyen látható, hogy például a téglalapokra nem igaz).
Statistics:
87 students sent a solution. 4 points: 56 students. 3 points: 22 students. 2 points: 5 students. 0 point: 2 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, November 2016
