Problem B. 4833. (December 2016)

B. 4833. For a sector of a circle of radius \(\displaystyle R\), smaller than a semicircle, the radius of the inscribed circle is \(\displaystyle r\), and the length of the chord connecting the endpoints of the boundary arc of the sector is \(\displaystyle 2a\). Prove that

\(\displaystyle \frac 1r= \frac 1R+ \frac 1a. \)

(3 pont)

Deadline expired on January 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen a körív középpontja \(\displaystyle K\), az ív két végpontja \(\displaystyle A\) és \(\displaystyle B\), az ív felezőpontja \(\displaystyle F\), a beírt kör középpontja az \(\displaystyle O\) pont, s végül a beírt kör érintési pontja a \(\displaystyle BK\) sugáron az \(\displaystyle E\) pont.

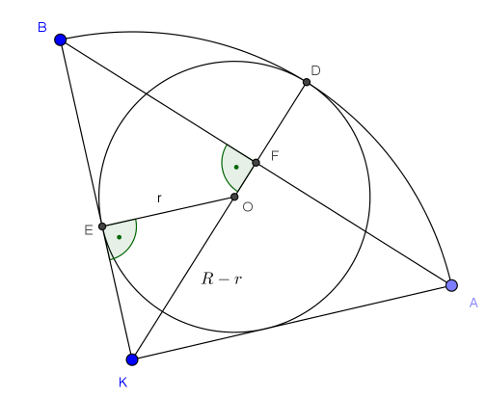
A \(\displaystyle BFK\) és \(\displaystyle OEK\) derékszögű háromszögek hasonlók, mert egyik hegyesszögük egybeeesik. Írjuk fel a megfelelő oldalak arányának egyenlőségét:

\(\displaystyle \frac{OE}{BF}=\frac{OK}{BK}.\)

Ugyanez a feladat szövegében szereplő jelölésekkel:

\(\displaystyle \frac{r}{a}=\frac{R-r}{R}.\)

Beszorzás és rendezés után

\(\displaystyle rR=aR-ar,\)

\(\displaystyle aR=rR+ar.\)

Elosztva az egyenlőség mindkét oldalát \(\displaystyle arR\)-rel éppen a bizonyítandó állítást kapjuk:

\(\displaystyle \frac{1}{r}=\frac{1}{R}+\frac{1}{a}.\)

Statistics:

122 students sent a solution.
3 points:	118 students.
2 points:	2 students.
1 point:	1 student.
0 point:	1 student.

Problems in Mathematics of KöMaL, December 2016