Problem B. 4836. (December 2016)

B. 4836. In a parallelogram \(\displaystyle ABCD\), \(\displaystyle BC=\lambda\, AB\). The intersection of the interior angle bisectors drawn from \(\displaystyle A\) and from \(\displaystyle B\) intersect at \(\displaystyle M\). What fraction of the parallelogram \(\displaystyle ABCD\) is covered by the triangle \(\displaystyle ABM\)?

(Proposed by J. Kozma, Szeged)

(5 pont)

Deadline expired on January 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldásvázlat. Az ábrán rendre 1-es, 2-es illetve 3-as indexszel jelöltük azokat az eseteket, amikor \(\displaystyle M\) a paralelogramma határán, azon kívül, illetve belül helyezkedik el. Az \(\displaystyle M\)-en át \(\displaystyle AD\)-vel húzott párhuzamos messe az \(\displaystyle AB\) oldalt \(\displaystyle F\)-ben. Az azonosan jelölt egy-, illetve kétíves szögek a szögfelező tulajdonság és váltószögek miatt egyenlőek. A kétszereseik összege \(\displaystyle 180^{\circ}\) lévén \(\displaystyle AMB\measuredangle = 90^{\circ}\); \(\displaystyle F\) az \(\displaystyle AB\) átfogójú derékszögű háromszög körülírt körének középpontja, így felezi az \(\displaystyle AB\) szakaszt. A keletkezett kisebb paralelogrammák és az egyenlőszárú háromszögek miatt például \(\displaystyle BC_1=MC_1=FB=AB/2\), ekkor \(\displaystyle \lambda = \dfrac{1}{2}\), és az \(\displaystyle ABM\) háromszög \(\displaystyle t\) területe fele az \(\displaystyle ABC_1D_1\) paralelogramma területének. Látható, hogy a 2-es helyzet \(\displaystyle \lambda < \dfrac{1}{2}\)-nek, a 3-as pedig \(\displaystyle \lambda > \dfrac{1}{2}\)-nek felel meg.

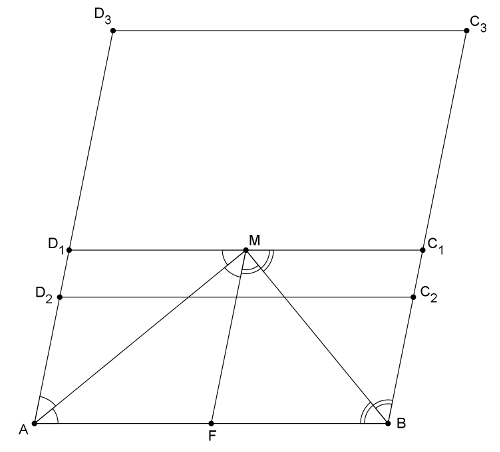
Az előbbi esetben a háromszög által lefedett terület \(\displaystyle t\left(1-\dfrac{C_1C_2^2}{C_1B^2}\right)=t\left(1-\dfrac{(AB(1/2 -\lambda))^2}{(AB/2)^2}\right)=4(\lambda -\lambda^2)t\), az \(\displaystyle ABC_2D_2\) paralelogramma \(\displaystyle 2t\dfrac{\lambda}{1/2}=4\lambda t\) területének \(\displaystyle 1-\lambda\)-szorosa.

Az utóbbi esetben a lefedett rész területe \(\displaystyle t\), ami az \(\displaystyle ABC_3D_3\) paralelogramma \(\displaystyle 2t\dfrac{\lambda}{1/2}=4\lambda t\) területének \(\displaystyle \dfrac{1}{4\lambda}\)-szorosa.

Statistics:

109 students sent a solution.
5 points:	55 students.
4 points:	3 students.
3 points:	47 students.
2 points:	3 students.
0 point:	1 student.

Problems in Mathematics of KöMaL, December 2016