Problem B. 4841. (January 2017)

B. 4841. The circle \(\displaystyle k\) centred at \(\displaystyle O\) intersects line \(\displaystyle e\) at points \(\displaystyle A\) and \(\displaystyle B\), and it intersects the perpendicular bisector of line segment \(\displaystyle OB\) at points \(\displaystyle C\) and \(\displaystyle D\). Prove that the angle bisector of angle \(\displaystyle COA \sphericalangle\) and line \(\displaystyle e\) enclose an angle of 60 degrees.

(3 pont)

Deadline expired on February 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A \(\displaystyle C\) és \(\displaystyle D\) pontok helyzete alapján két különböző ábra rajzolható meg, de a megoldás mindkét esetben ugyanaz.

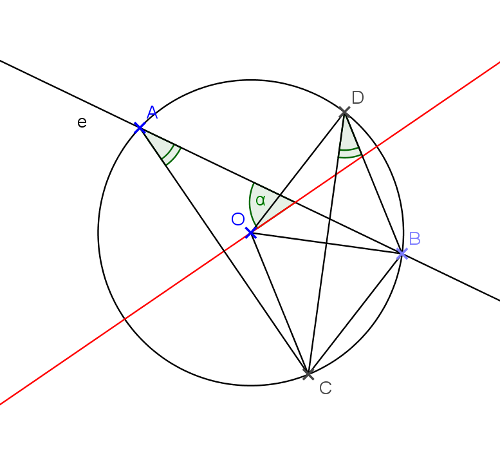
Legyen az \(\displaystyle OB\) sugár felezőpontja \(\displaystyle F\). A felezőmerőleges a körvonalat metszi a \(\displaystyle C\) és \(\displaystyle D\) pontokban, emiatt a \(\displaystyle COF\) és \(\displaystyle DOF\) háromszögek félszabályosak, \(\displaystyle ODF\angle=ODC\angle=OCD\angle=30^{\circ}.\) A \(\displaystyle CAB\angle\) és a \(\displaystyle CDB\angle\) a \(\displaystyle BC\) íven nyugvó kerületi szögek, vagyis a \(\displaystyle CA\) egyenes \(\displaystyle 30^{\circ}\)-os szöget zár be az \(\displaystyle AB\) húr \(\displaystyle e\) egyenesével. Az \(\displaystyle AC\)-re állított merőlegesek, köztük a \(\displaystyle COA\angle\) szögfelezője, ezért \(\displaystyle 60^{\circ}\)-os szöget zárnak be vele.

Statistics:

115 students sent a solution.
3 points:	108 students.
2 points:	3 students.
1 point:	4 students.

Problems in Mathematics of KöMaL, January 2017