 |
A B. 4849. feladat (2017. február) |
B. 4849. Az \(\displaystyle ABC\triangle\) beírt körének középpontja \(\displaystyle K\), az \(\displaystyle AB\) oldalhoz hozzáírt kör középpontja \(\displaystyle L\). Mutassuk meg, hogy a körülírt kör \(\displaystyle C\)-vel szemközti \(\displaystyle AB\) íve és a \(\displaystyle KL\) szakasz felezik egymást.
(3 pont)
A beküldési határidő 2017. március 10-én LEJÁRT.
Megoldás. A \(\displaystyle C\)-hez tartozó belső szögfelező felezi a körülírt kör \(\displaystyle AB\) ívét, mert két egyenlő kerületi szöghöz egy körben egyenlő ívek tartoznak. Az \(\displaystyle AB\) szakasz felezőmerőlegese is felezi az \(\displaystyle AB\) ívet, hiszen az \(\displaystyle AB\) szakasz és a kör is tengelyesen szimmetrikus erre a felezőmerőlegesre. A \(\displaystyle C\)-hez tartozó belső szögfelező és az \(\displaystyle AB\) szakasz felezőmerőlegese tehát az \(\displaystyle AB\) ív \(\displaystyle F\) felezőpontjában metszik egymást.
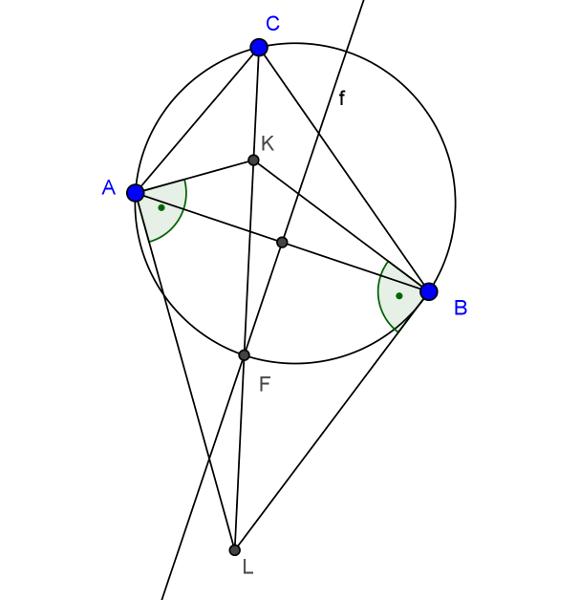
Az \(\displaystyle A\) és \(\displaystyle B\) csúcsokhoz tartozó külső szögfelezők és a \(\displaystyle C\)-hez tartozó belső szögfelező az \(\displaystyle AB\) oldalhoz hozzáírt kör \(\displaystyle L\) középpontjában metszik egymást. Vagyis \(\displaystyle KL\) egyenese a \(\displaystyle C\)-hez tartozó belső szögfelező. Másrészt az \(\displaystyle A\) és \(\displaystyle B\) csúcsokhoz tartozó belső és külső szögfelezők merőlegesek egymásra, \(\displaystyle KAL\angle =LBK\angle=90^{\circ}\). Emiatt az \(\displaystyle A\) és \(\displaystyle B\) pontok a \(\displaystyle KL\) szakasz Thálesz-körén helyezkednek el. Ennek a körnek \(\displaystyle KL\) átmérője, az \(\displaystyle AB\) pedig húrja. A húr felezőmerőlegese átmegy a kör középpontján, ami a \(\displaystyle KL\) szakasz felezőpontja. Tehát az \(\displaystyle F\) pont a \(\displaystyle KL\) felezőpontja is.
Statisztika:
101 dolgozat érkezett. 3 pontot kapott: 84 versenyző. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 9 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2017. februári matematika feladatai

