Problem B. 4858. (March 2017)

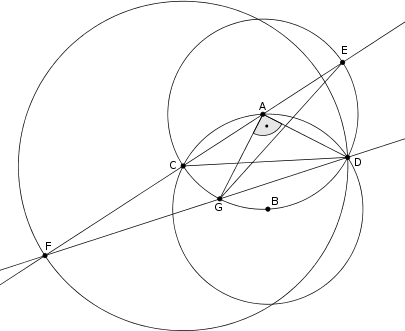
B. 4858. Points \(\displaystyle A\) and \(\displaystyle B\) are separated by a unit distance. The unit circles \(\displaystyle k_A\) and \(\displaystyle k_B\) centred at \(\displaystyle A\) and \(\displaystyle B\) intersect at points \(\displaystyle C\) and \(\displaystyle D\), respectively. Let \(\displaystyle k_C\) denote the circle centred at \(\displaystyle C\) and passing through \(\displaystyle D\). \(\displaystyle F\) is that intersection of line \(\displaystyle AC\) and circle \(\displaystyle k_C\) which is farther away from \(\displaystyle A\). \(\displaystyle G\) is the other intersection of circle \(\displaystyle k_A\) and line \(\displaystyle DF\). Show that \(\displaystyle \angle GAD=90^\circ\).

(3 pont)

Deadline expired on April 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk az ábra jelöléseit. Mivel \(\displaystyle ABC\) és \(\displaystyle ADB\) egyenlő oldalúak, ezért az \(\displaystyle ACD\) egyenlőszárú háromszögben \(\displaystyle A\angle=120^\circ\) és \(\displaystyle C\angle=D\angle=30^\circ\). Így a \(\displaystyle CFD\) egyenlőszárú háromszögben \(\displaystyle C\angle=150^{\circ}\) és \(\displaystyle D\angle=15^\circ\). A \(\displaystyle k_A\) kör \(\displaystyle CG\) íven nyugvó kerületi szögei \(\displaystyle GDC\angle=CEG\angle=15^\circ\), s így \(\displaystyle GAE\) egyenlőszárú háromszögben \(\displaystyle A\angle=150^\circ\). Mivel a \(\displaystyle DAE\triangle\) szabályos, \(\displaystyle GAD\angle=GAE\angle-DAE\angle=150^\circ-60^\circ=90^\circ\), ahogy állítottuk.

Statistics:

105 students sent a solution.
3 points:	98 students.
2 points:	6 students.
0 point:	1 student.

Problems in Mathematics of KöMaL, March 2017