Problem B. 4861. (March 2017)

B. 4861. Let \(\displaystyle r\) and \(\displaystyle R\), respectively, denote the radii of the inscribed and circumscribed circles of a right-angled triangle \(\displaystyle ABC\). Let \(\displaystyle CD\) be the altitude drawn to the hypotenuse \(\displaystyle AB\). Draw the square \(\displaystyle CEFG\) of side length \(\displaystyle CD\) that has vertex \(\displaystyle E\) on side \(\displaystyle AC\) and vertex \(\displaystyle G\) on side \(\displaystyle BC\). Let \(\displaystyle T\) and \(\displaystyle t\), respectively, denote the parts of the area of the square \(\displaystyle CEFG\) which lie inside and outside the triangle \(\displaystyle ABC\). Prove that

\(\displaystyle \frac{t}{T}=\frac{r}{2R}. \)

(B. Bíró, Eger)

(4 pont)

Deadline expired on April 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyenek az \(\displaystyle ABC\) háromszög oldalai a szokásos módon \(\displaystyle a=BC\), \(\displaystyle b=AC\) és \(\displaystyle c=AB\). A különböző sokszögek területét \(\displaystyle \mathrm{ter}(\dots)\) fogja jelölni.

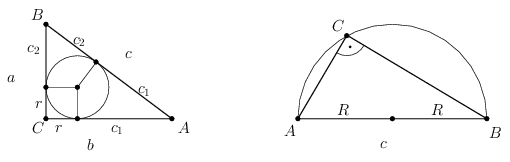
Jól ismert, és a csúcsokból a beírt körhöz húzott érintő szakaszok egyenlőségéből leolvasható, hogy \(\displaystyle a+b-c=2r\). A Thalész-tétel megfordításából tudjuk, hogy \(\displaystyle c=2R\).

Legyen az \(\displaystyle AB\) szakasz metszéspontja az \(\displaystyle FG\), illetve az \(\displaystyle EF\) szakasszal \(\displaystyle P\), illetve \(\displaystyle Q\). Az \(\displaystyle ABC\) háromszög hasonló a \(\displaystyle PQF\) háromszöghöz, mert a megfelelő oldalaik párhuzamosak. Legyen a hasonlóság aránya \(\displaystyle h=\frac{PQ}{AB}=\frac{QF}{BC}=\frac{FP}{CA}\); ekkor tehát

\(\displaystyle QF = h\cdot BC = ha, \quad FP = h\cdot CA = hb, \quad PQ = h\cdot AB = hc = 2hR. \)

Legyen \(\displaystyle m=CD\). A feltétel szerint \(\displaystyle CE=CG=CD=m\), ezért a \(\displaystyle C\) középpontú, \(\displaystyle m\) sugarú kör az \(\displaystyle E\), a \(\displaystyle G\), illetve a \(\displaystyle D\) pontban érinti az \(\displaystyle EF\), \(\displaystyle FG\) és \(\displaystyle AB\) egyeneseket. A \(\displaystyle CEQD\) és a \(\displaystyle CDPG\) négyszögek deltoidok, területüket felezi a \(\displaystyle CQ\), illetve a \(\displaystyle CP\) átlójuk.

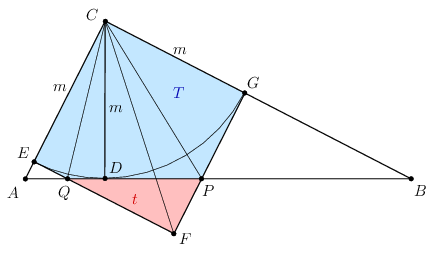
Fejezzük ki a \(\displaystyle t\) és \(\displaystyle T\) területeket az oldalakkal, a \(\displaystyle h\) aránnyal és az \(\displaystyle m\) magassággal, valamint az \(\displaystyle r\) és \(\displaystyle R\) sugarakkal a következőképpen:

\(\displaystyle t = \mathrm{ter}(FPQ) = \mathrm{ter}(CQF)+\mathrm{ter}(CFP)-\mathrm{ter}(CQP) = \frac{QF\cdot m}2 + \frac{FP\cdot m}2 - \frac{PQ\cdot m}2 = \frac{h(a+b-c)m}2 = hrm, \)

\(\displaystyle T = \mathrm{ter}(CEQPG) = \mathrm{ter}(CEQD)+\mathrm{ter}(CDPG) = 2\mathrm{ter}(CQD)+2\mathrm{ter}(CDP) = 2\mathrm{ter}(CQP) = PQ \cdot m = 2hRm. \)

A két terület hányadosa

\(\displaystyle \frac{t}{T} = \frac{hrm}{2hRm} = \frac{r}{2R}. \)

Statistics:

64 students sent a solution.
4 points:	56 students.
3 points:	3 students.
2 points:	3 students.
1 point:	1 student.
0 point:	1 student.

Problems in Mathematics of KöMaL, March 2017