 Problem B. 4862. (March 2017)
Problem B. 4862. (March 2017)
B. 4862. \(\displaystyle M\), \(\displaystyle N\), \(\displaystyle P\), \(\displaystyle Q\), and \(\displaystyle R\), respectively, are the midpoints of the sides \(\displaystyle AB\), \(\displaystyle BC\), \(\displaystyle CD\), \(\displaystyle DE\) and \(\displaystyle EA\) of a convex pentagon \(\displaystyle ABCDE\). Show that if the line segments \(\displaystyle AP\), \(\displaystyle BQ\), \(\displaystyle CR\) and \(\displaystyle DM\) are concurrent then the common point also lies on line segment \(\displaystyle EN\).
(S. Róka, Nyíregyháza)
(5 pont)
Deadline expired on April 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás:
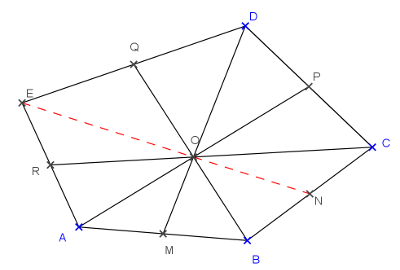
A közös metszéspont legyen \(\displaystyle O\). Az \(\displaystyle O\)-ból az \(\displaystyle A\)-ba vezető vektort jelölje \(\displaystyle \underline{a}\), és hasonló a többi jelölés is. Mivel \(\displaystyle O\) rajta van az \(\displaystyle AP\) szakaszon, így a két vektor vektoriális szorzata nulla: \(\displaystyle \underline{a}\times \underline{p}=\underline{0}\). A \(\displaystyle CD\) szakasz felezőpontja \(\displaystyle P\), így
\(\displaystyle \underline{0}=\underline{a}\times \underline{p}=\underline{a}\times \frac{\underline{c}+\underline{d}}{2}=\frac{\underline{a}\times \underline{c}+\underline{a}\times \underline{d}}{2}.\)
A vektoriális szorzás tulajdonsága miatt tehát \(\displaystyle \underline{a}\times \underline{c}=\underline{d}\times \underline{a}\). Hasonlóan kapjuk, hogy \(\displaystyle \underline{b}\times \underline{d}=\underline{e}\times \underline{b}\), \(\displaystyle \underline{c}\times \underline{e}=\underline{a}\times \underline{c}\), \(\displaystyle \underline{d}\times \underline{a}=\underline{b}\times \underline{d}\). Ezekből egyenlőségeken át sorra haladva eljutunk az \(\displaystyle \underline{e}\times \underline{b}=\underline{c}\times \underline{e}\) következtetéshez, hiszen
\(\displaystyle \underline{e}\times \underline{b}=\underline{b}\times \underline{d}=\underline{d}\times \underline{a}=\underline{a}\times \underline{c}=\underline{c}\times \underline{e}.\)
A bizonyítandó állítás:
\(\displaystyle \underline{0}=\underline{e}\times \underline{n}=\underline{e}\times \frac{\underline{b}+\underline{c}}{2}=\frac{\underline{e}\times \underline{b}+\underline{e}\times \underline{c}}{2},\)
és ez valóban teljesül, mert előbb megállapítottuk az \(\displaystyle \underline{e}\times \underline{b}=\underline{c}\times \underline{e}\) egyenlőséget.
Megjegyzés. Elemi úton is célhoz lehet jutni. Ilyen megoldást majd a nyomtatott lapban fogunk közölni.
Statistics:
33 students sent a solution. 5 points: Baran Zsuzsanna, Borbényi Márton, Busa 423 Máté, Csiszár Zoltán, Fülöp Anna Tácia, Gáspár Attila, Győrffy Ágoston, Imolay András, Janzer Orsolya Lili, Kerekes Anna, Kővári Péter Viktor, Nagy Nándor, Schrettner Jakab, Szabó 417 Dávid, Szemerédi Levente, Tanács Viktória, Tóth Viktor, Tubak Dániel, Weisz Máté. 4 points: Döbröntei Dávid Bence, Kocsis Júlia, Laki 37 Dániel, Németh 123 Balázs, Szabó Kristóf, Török Ádám. 1 point: 3 students. 0 point: 5 students.
Problems in Mathematics of KöMaL, March 2017
