Problem B. 4863. (March 2017)

B. 4863. In a triangle \(\displaystyle ABC\), \(\displaystyle AB=BC\). \(\displaystyle D\) is an interior point of the triangle such that \(\displaystyle \angle ADC= 2 \angle ABC\). Prove that the distance of point \(\displaystyle B\) from the exterior angle bisector of \(\displaystyle \angle ADC\) is the arithmetic mean of the line segments \(\displaystyle AD\) and \(\displaystyle DC\).

(Kvant)

(5 pont)

Deadline expired on April 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

1. megoldás.

,,Szögfelezőre tükrözni kell.'' (Bohner Géza)

Legyen a körülírt kör középpontja \(\displaystyle O\), és legyen \(\displaystyle f\) az \(\displaystyle ADC\sphericalangle\) külső szögfelezője. Mivel \(\displaystyle ADC\angle=2ABC\angle=AOC\angle\), a \(\displaystyle D\) pont az \(\displaystyle AOC\) köríven van. Jól ismert, hogy az \(\displaystyle ADC\angle\) külső szögfelezője átmegy az \(\displaystyle \widehat{ADC}\) körívet felező ponton, vagyis \(\displaystyle f\) átmegy \(\displaystyle O\)-n.

Legyen \(\displaystyle B\) vetülete az \(\displaystyle f\) egyenesen \(\displaystyle T\), és legyen \(\displaystyle A\) és \(\displaystyle B\) tükörképe \(\displaystyle f\)-re \(\displaystyle A'\), illetve \(\displaystyle B'\). Mivel \(\displaystyle f\) átmegy a kör középpontján, \(\displaystyle A'\) és \(\displaystyle B'\) is a körülírt körön van. Továbbá, mivel \(\displaystyle A\) és \(\displaystyle A'\) egymás tükörképei a külső szögfelezőre, \(\displaystyle DA'\) a \(\displaystyle CD\) szakasz meghosszabbítása. A \(\displaystyle T\) pont a \(\displaystyle BB'\) szakasz felezőpontja, és \(\displaystyle AA' \| BB'\).

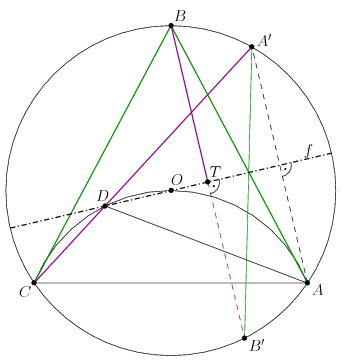
A feltétel szerint \(\displaystyle BC=AB\), így az \(\displaystyle \widehat{AB}\) és \(\displaystyle \widehat{BC}\) körívek ugyanakkorák és azonos irányításúak. Az \(\displaystyle \widehat{AB}\) és \(\displaystyle \widehat{A'B'}\) körívek egymás \(\displaystyle f\)-re vonatkozó tükörképei, így az \(\displaystyle \widehat{AB}\) és \(\displaystyle \widehat{B'A'}\) körívek is ugyanakkorák és azonos irányításúak. Az \(\displaystyle O\) körül az \(\displaystyle AOB\sphericalangle\) szöggel elforgatva az \(\displaystyle A,B,B'\) pontokat, azok képei rendre az \(\displaystyle B,C,A'\) pontok, tehát például \(\displaystyle BB'=CA'\). Ezért

\(\displaystyle CD+AD = CD+DA' = CA' = BB' = 2BT, \)

\(\displaystyle BT = \frac{CD+AD}{2}. \)

2. megoldás. Legyen ismét \(\displaystyle O\) a körülírt kör középpontja és \(\displaystyle f\) az \(\displaystyle ADC\sphericalangle\) külső felezője, ami átmegy \(\displaystyle O\)-n, és legyen \(\displaystyle T\) a \(\displaystyle B\) pont vetülete az \(\displaystyle f\) egyenesen. Legyen \(\displaystyle r\) a körülírt kör sugara, és legyen az \(\displaystyle AOC\) körben \(\displaystyle O'\) az \(\displaystyle O\)-val átellenes pont. Ekkor \(\displaystyle AO'=CO'\).

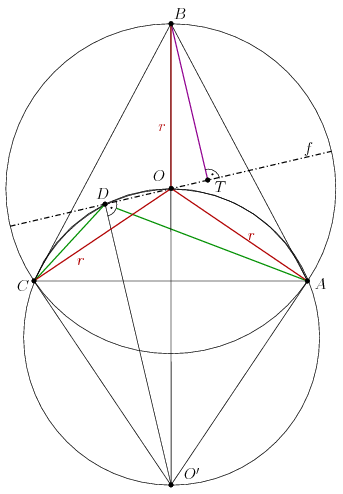
Felhasználva az \(\displaystyle ADCO'\) és az \(\displaystyle AOCO'\) négyszögre felírt Ptolemaiosz-tételt, valamint azt, hogy az \(\displaystyle OTB\) és \(\displaystyle ODO'\) derékszögű háromszögek hasonlók:

\(\displaystyle \frac{AD + CD}{2r} = \frac{AD + CD}{AO + CO} = \frac{AD \cdot CO' + CD \cdot AO'}{AO \cdot CO' + CO \cdot AO'} = \frac{DO' \cdot AC}{OO'\cdot AC} = \frac{DO'}{OO'} = \frac{TB}{OB} = \frac{BT}{r}, \)

\(\displaystyle \frac{AD + CD}{2} = BT. \)

Statistics:

46 students sent a solution.
5 points:	Alexy Milán, Asztalos Ádám, Baran Zsuzsanna, Beke Csongor, Borbényi Márton, Busa 423 Máté, Csahók Tímea, Döbröntei Dávid Bence, Fekete Balázs Attila, Fülöp Anna Tácia, Gáspár Attila, Győrffy Ágoston, Harsányi Benedek, Horváth Péter, Imolay András, Kerekes Anna, Kocsis Júlia, Kőrösi Ákos, Kővári Péter Viktor, Lukács Lilla Réka, Marshall Tamás, Márton Dénes, Mészáros Anna, Nagy Nándor, Németh 123 Balázs, Olosz Adél, Pap Benedek, Póta Balázs, Schrettner Jakab, Simon Dániel Gábor, Szabó 417 Dávid, Szabó Kristóf, Szécsényi Nándor, Szemerédi Levente, Tiderenczl Dániel, Velkey Vince, Weisz Máté.
4 points:	Csiszár Zoltán, Deák Bence, Lakatos Ádám, Zólomy Kristóf.
3 points:	2 students.
1 point:	1 student.
0 point:	2 students.

Problems in Mathematics of KöMaL, March 2017