 Problem B. 4865. (March 2017)
Problem B. 4865. (March 2017)
B. 4865. In an acute-angled triangle, \(\displaystyle f\) and \(\displaystyle g\) are the line segments that divide the angle enclosed by sides \(\displaystyle a\) and \(\displaystyle b\) into three equal parts. Prove that
\(\displaystyle \frac{f+g}{2}< \frac{2}{\frac{1}{a} +\frac{1}{b}}. \)
(6 pont)
Deadline expired on April 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
1. Megoldás. Használjuk a szokásos jelöléseket, és legyen a \(\displaystyle \gamma\) szög felelzője \(\displaystyle e\). Az ismert formula szerint
\(\displaystyle e=\frac {2ab \cos\frac{\gamma}{2}}{a+b}.\)
Ugyanígy, mivel \(\displaystyle e\) az \(\displaystyle f\) és \(\displaystyle g\) szögét is felezi:
\(\displaystyle e=\frac {2fg \cos\frac{\gamma}{6}}{f+g}.\)
Ezt felhasználva a bizonyítandó a következő alakba írható:
\(\displaystyle \frac{f+g}{2}\cos\frac\gamma 2< \frac 2 {\frac 1f + \frac 1g}\cos \frac \gamma 6.\)
Bevezetve a \(\displaystyle \gamma/6=x\) jelölést, és rendezve a két oldalt kapjuk, hogy
\(\displaystyle (f+g)\left ( \frac 1f + \frac 1g \right ) < 4\cdot\frac{\cos x}{\cos 3x},\)
vagyis
\(\displaystyle \frac fg +\frac gf< 4\cdot\frac{\cos x}{\cos 3x}-2.\)
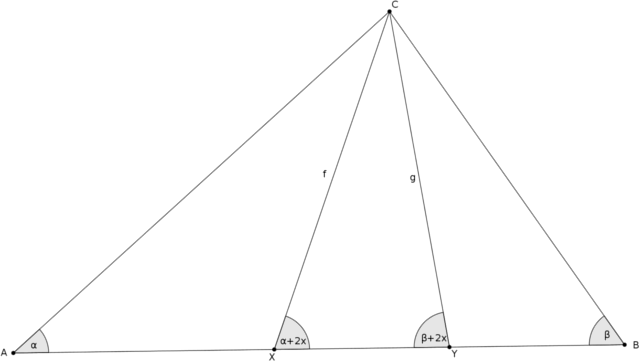
Rögzítsük \(\displaystyle x<15^\circ\) értékét, és vizsgáljuk a bal oldalt. Feltehető, hogy \(\displaystyle f\geq g\) (vagyis \(\displaystyle \alpha\leq \beta\)), s ekkor a bal oldal \(\displaystyle f/g\)-ben monoton nő. Legyen \(\displaystyle y=\alpha+2x\), mivel \(\displaystyle 90^\circ>\beta=180^\circ-y-4x\), így \(\displaystyle 90^\circ-4x<y<120^\circ\).
Alkalmazzuk a szinusz-tételt az \(\displaystyle XYC\triangle\)-ben: \(\displaystyle f/g=\sin(\beta+2x)/\sin(\alpha+2x)=\sin(y+2x)/\sin y=\cos 2x+ \ctg y \cdot \sin 2x\). Mivel \(\displaystyle \ctg y\) monoton fogyó, így \(\displaystyle f/g<\cos 2x+ \ctg (90^\circ-4x) \cdot \sin 2x=\sin (90^\circ-2x)/ \sin (90^\circ-4x)=\cos 2x / \cos 4x\). Mindezekből következik, hogy
\(\displaystyle \frac fg +\frac gf< \frac {\cos 2x}{\cos 4x}+ \frac {\cos 4x}{\cos 2x}.\)
Elegendő igazolni tehát, hogy
\(\displaystyle \frac {\cos 2x}{\cos 4x}+ \frac {\cos 4x}{\cos 2x} \leq 4\cdot\frac{\cos x}{\cos 3x}-2.\)
Vezessük be a \(\displaystyle t=\cos 2x\) jelölést. Világos, hogy \(\displaystyle \sqrt 3/2=\cos 30^\circ < t < 1\). Kihasználva a \(\displaystyle \cos 3x=4\cos^3x-3 \cos x=\cos x(2\cos 2x -1)\), valamint a \(\displaystyle \cos 4x= 2(\cos 2x)^2-1\) azonosságokat a bizonyítandó így alakul:
\(\displaystyle \frac t {2t^2-1}+ \frac {2t^2-1}t\leq \frac 4{2t-1}-2.\)
Közös nevezőre hozva, felszorozva, rendezve és a \(\displaystyle t-1\) gyöktényezőt kiemelve:
\(\displaystyle (t-1)(8t^4+12t^3- 6t^2-7t+1)\leq 0\)
egyenlőtlenséget kell igazolnunk \(\displaystyle \sqrt 3 /2 <t<1\) feltétel mellett. De \(\displaystyle 8t^4>8t^2\cdot 3/4=6t^2\), és \(\displaystyle 12t^3>12t\cdot 3/4=9t\) miatt a megadott intervallumon a második tényező pozitív, míg \(\displaystyle t-1\) triviálisan negatív. Mivel a lépéseink megfordíthatóak, ezért az állítást beláttuk.
2. Megoldás(vázlat). Ha a magasság egységnyi, \(\displaystyle x=\frac\gamma6\), \(\displaystyle \alpha=m-3x\) és \(\displaystyle \pi-\beta=m+3x\), akkor \(\displaystyle a=\frac1{\sin(m-3x)}\), \(\displaystyle b=\frac1{\sin(m+3x)}\), \(\displaystyle f=\frac1{\sin(m-x)}\) és \(\displaystyle g=\frac1{\sin(m+x)}\).
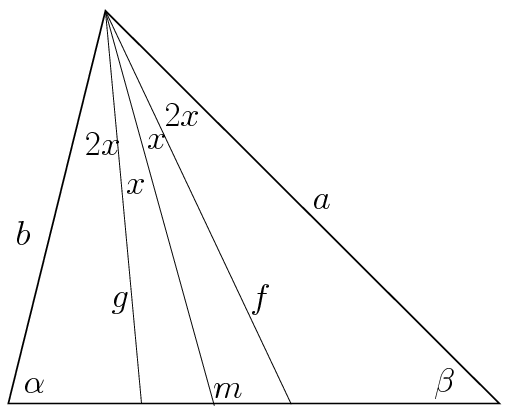
Behelyettesítve, az állítás:
\(\displaystyle \dfrac{\dfrac1{\sin(m+x)}+\dfrac1{\sin(m-x)}}2 \stackrel{?}{<} \frac2{\sin(m+3x)\sin(m-3x)}. \)
Átszorozva, kibontva, \(\displaystyle \cos m\cos x\)-szel osztva majd gyököt vonva:
\(\displaystyle 1 \stackrel{?}{<} 2\cos x \cdot \big|\tg m\big|. \)
Ez pedig igaz, mert \(\displaystyle \frac\pi4<m<\frac{3\pi}4\) és \(\displaystyle x<\frac\pi{12}\).
Statistics:
18 students sent a solution. 6 points: Beke Csongor, Borbényi Márton, Csahók Tímea, Daróczi Sándor, Gáspár Attila, Imolay András, Kerekes Anna, Kővári Péter Viktor, Németh 123 Balázs, Szabó Kristóf, Tóth Viktor. 5 points: Vári-Kakas Andor. 4 points: 1 student. 2 points: 4 students. 0 point: 1 student.
Problems in Mathematics of KöMaL, March 2017
