Problem B. 4873. (April 2017)

B. 4873. In a triangle \(\displaystyle ABC\), \(\displaystyle AB=1\), \(\displaystyle \angle BAC =135^{\circ}\), \(\displaystyle \angle ABC =30^{\circ}\). Find the parameter of the parabola with symmetry axis \(\displaystyle AB\) that is tangent to the lines \(\displaystyle AC\) and \(\displaystyle BC\).

(5 pont)

Deadline expired on May 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

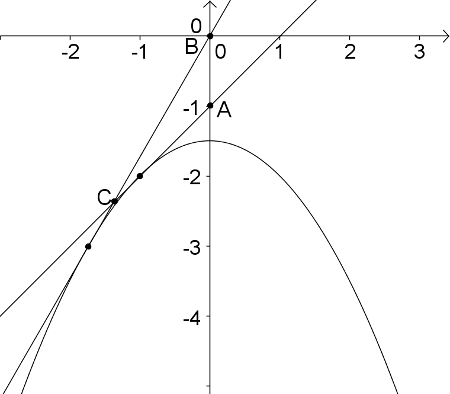
Megoldás. Legyen a koordinátarendszer origója \(\displaystyle B\), az \(\displaystyle y\)-tengely pedig az \(\displaystyle AB\) egyenes. Az \(\displaystyle A\) pont koordinátái válaszhatók \(\displaystyle (0;-1)\)-nek. Az 1 meredekségű \(\displaystyle AC\) egyenes egyenlete \(\displaystyle y=x-1\), a \(\displaystyle \tg 60^{\circ} = \sqrt{3}\) meredekségű \(\displaystyle BC\) egyenes egyenlete pedig \(\displaystyle y=\sqrt{3}x\). Ha a keresett parabola egyenlete

\(\displaystyle y=-\dfrac{1}{2p}x^2 + a, \)

akkor a \(\displaystyle -\dfrac{1}{2p}x^2 + a = x-1\) és a \(\displaystyle -\dfrac{1}{2p}x^2 + a = \sqrt{3}x\) egyenleteknek egyetlen megoldása van, azaz \(\displaystyle D_1= 1-4\cdot \dfrac{1}{2p}(-1-a)=0\) és \(\displaystyle D_2=3-4\cdot \dfrac{1}{2p}(-a)=0\). Ebből \(\displaystyle 0=D_1-D_2=-2 + \dfrac{2}{p}\), azaz \(\displaystyle p=1\) a parabola paramétere (és \(\displaystyle a=-1,5\)).

Statistics:

61 students sent a solution.
5 points:	Baran Zsuzsanna, Csahók Tímea, Csiszár Zoltán, Csuha Boglárka, Daróczi Sándor, Döbröntei Dávid Bence, Fekete Balázs Attila, Fitos Bence, Fülöp Anna Tácia, Gáspár Attila, Geretovszky Anna, György Levente, Horváth Péter, Imolay András, Janzer Orsolya Lili, Kocsis Júlia, Kovács 654 Áron , Kővári Péter Viktor, Marshall Tamás, Mikulás Zsófia, Nagy Nándor, Noszály Áron, Olosz Adél, Páli Petra, Paulovics Péter, Póta Balázs, Richlik Róbert, Saár Patrik, Sáfi Lilla, Scheidler Barnabás, Szabó 121 Csaba, Szécsényi Nándor, Tiderenczl Dániel, Tiszay Ádám, Tóth 111 Máté , Tóth 827 Balázs, Török Tímea, Tubak Dániel, Várkonyi Dorka, Weisz Máté, Zólomy Kristóf.
4 points:	11 students.
2 points:	9 students.

Problems in Mathematics of KöMaL, April 2017