Problem B. 4877. (May 2017)

B. 4877. Points \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) and \(\displaystyle D\), in this order, lie on a straight line. Point \(\displaystyle E\) does not lie on the line, and

\(\displaystyle AEB\sphericalangle=BEC\sphericalangle =CED\sphericalangle = 45^\circ. \)

Let \(\displaystyle F\) and \(\displaystyle G\) be the midpoints of \(\displaystyle AC\) and \(\displaystyle BD\), respectively. What is the measure of angle \(\displaystyle FEG\)?

Proposed by the class 11C of Fazekas Gimnázium, Budapest

(3 pont)

Deadline expired on June 12, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás.

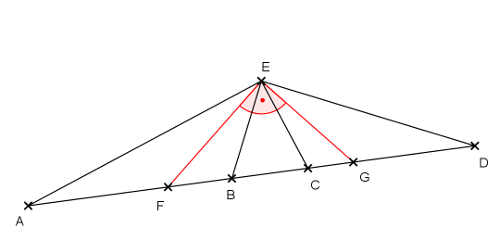
Megmutatjuk, hogy az \(\displaystyle FEG\) szög derékszög. Legyen \(\displaystyle EAB\sphericalangle =\alpha\). Ezt felhasználva már kiszámíthatók az ábrán látható további szögek. Az \(\displaystyle E\) pont rajta van az \(\displaystyle AC\) Thalész-körén, így az \(\displaystyle F\) pont, a kör középpontja egyenlő távolságra van az \(\displaystyle A\), \(\displaystyle C\) és \(\displaystyle E\) pontoktól. Az \(\displaystyle AFE\) háromszög egyenlő szárú, az \(\displaystyle F\)-nél lévő külső szöge \(\displaystyle EFB \sphericalangle =2\alpha\). Az \(\displaystyle AEB\) háromszögben \(\displaystyle AEB \sphericalangle =45^{\circ}\), emiatt a \(\displaystyle B\)-nél fekvő külső szög \(\displaystyle EBD\sphericalangle =45^{\circ}+\alpha\).

Másrészt a \(\displaystyle BED\) háromszög is derékszögű, tehát \(\displaystyle EDB\sphericalangle =45^{\circ}-\alpha\). A \(\displaystyle BD\) szakasz Thalész-körének \(\displaystyle G\) középpontja egyenlő távolságra van a \(\displaystyle B, D\) és \(\displaystyle E\) pontoktól. Az \(\displaystyle EGD\) egyenlő szárú háromszög \(\displaystyle G\)-nél fekvő külső szöge a \(\displaystyle D\)-nél lévő belső szög kétszerese, \(\displaystyle EGF\sphericalangle =90^{\circ}-2\alpha\). Beláttuk, hogy az \(\displaystyle FEG\) háromszög két szögének összege \(\displaystyle 90^{\circ}\), tehát az \(\displaystyle FEG\) szög valóban derékszög.

Statistics:

70 students sent a solution.
3 points:	67 students.
2 points:	2 students.
1 point:	1 student.

Problems in Mathematics of KöMaL, May 2017