 Problem C. 1012. (December 2009)
Problem C. 1012. (December 2009)
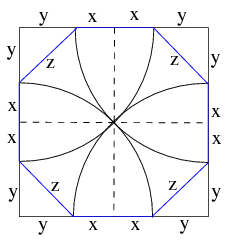
C. 1012. A circle passing through the centre of a square is drawn about each vertex. The circles intersect the sides of the square at 8 points altogether. Prove that the intersections form a regular octagon.
(5 pont)
Deadline expired on January 11, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Legyen a négyzet oldalának hossza 2 egység. Ekkor a berajzolt körök sugara \(\displaystyle \sqrt 2\). Egy oldalon az oldal felezőpontja és a körvonal \(\displaystyle x=\sqrt 2 -1\) távolságra vannak, ugyanazon pont a körön a csúcstól \(\displaystyle y=2-\sqrt 2\) távolságra van. Egy csúcshoz legközelebb eső metszéspontok távolsága \(\displaystyle z= \sqrt 2 (2 - \sqrt 2) = 2(\sqrt 2 - 1)\). A metszéspontok által meghatározott nyolcszög oldalainak hossza \(\displaystyle 2x\), ha az oldal a négyzet oldalára esik, illetve \(\displaystyle z\). Mivel mindkettő \(\displaystyle 2(\sqrt 2 - 1)\), és a nyolcszög minden szöge egyenlő a szimmetriák miatt, ezért a metszéspontok valóban egy szabályos nyolcszög csúcsai.
Statistics:
307 students sent a solution. 5 points: 133 students. 4 points: 100 students. 3 points: 16 students. 2 points: 11 students. 1 point: 30 students. 0 point: 7 students. Unfair, not evaluated: 10 solutionss.
Problems in Mathematics of KöMaL, December 2009
