Problem C. 1013. (December 2009)

C. 1013. Represent the set of points (x,y) in the coordinate plane the coordinates of which satisfy the two conditions below: x²+y²25, .

(5 pont)

Deadline expired on January 11, 2010.

Sorry, the solution is available only in Hungarian. Google translation

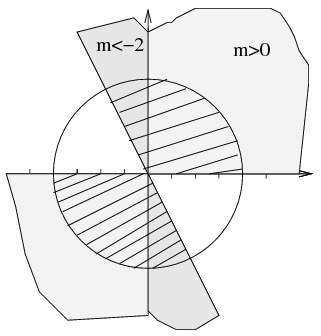
Megoldás. \(\displaystyle x^2 + y^2 \le 2\) az origó középpontú, \(\displaystyle \sqrt 2\) sugarú körlap pontjainak koordinátáira teljesül. \(\displaystyle -1\le \frac{x}{x+y}\le 1\) teljesül, ha \(\displaystyle x=0\). Legyen \(\displaystyle m=\frac yx\), ha \(\displaystyle x\ne 0\)-val egyszerűsítve a \(\displaystyle -1\le \frac{1}{1+m}\le 1\) egyenlőtlenségeket vizsgáljuk. \(\displaystyle \frac{1}{1+m}\le 1\) akkor teljesül, ha \(\displaystyle m\ge 0\) vagy \(\displaystyle m< -1\). \(\displaystyle -1\le \frac{1}{1+m}\) pontosan akkor teljesül, ha \(\displaystyle 0\le \frac{2+m}{1+m}\), azaz \(\displaystyle 2+m\ge 0\) és \(\displaystyle 1+m>0\) vagy \(\displaystyle 2+m\le 0\) és \(\displaystyle 1+m<0\). Az első \(\displaystyle m>-1\) esetén teljesül, a második eset akkor, ha \(\displaystyle m\le -2\). Az eredeti egyenlőtlenségek egyszerre akkor teljesülnek, ha \(\displaystyle m\ge 0\) vagy \(\displaystyle m\le -2\) és \(\displaystyle x\ne 0\). A pontok a két csíkozott körcikk belsejében és határárán vannak az origó kivételével.

Statistics:

199 students sent a solution.
5 points:	78 students.
4 points:	50 students.
3 points:	19 students.
2 points:	14 students.
1 point:	19 students.
0 point:	13 students.
Unfair, not evaluated:	6 solutionss.

Problems in Mathematics of KöMaL, December 2009