 Problem C. 1017. (January 2010)
Problem C. 1017. (January 2010)
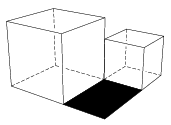
C. 1017. The two cubes shown in the diagram are lying on a horizontal tabletop. The sum of their edges is 2 cm, and the sum of their volumes is 5.375 cm3. Find the area of the black rectangle.
(5 pont)
Deadline expired on February 10, 2010.
Sorry, the solution is available only in Hungarian. Google translation
1. megoldás. A következő egyenletrendszer alapján keressük \(\displaystyle ab\)-t:
\(\displaystyle a+b=2\)
\(\displaystyle a^3 + b^3 =5,375.\)
Mivel \(\displaystyle a^3 + b^3 = (a+b)^3 - 3ab(a+b)\), ezért \(\displaystyle ab=\frac{2^3 - 5,357}{3\cdot 2}=0,4375\). Tehát a fekete téglalap területe \(\displaystyle 0,4375\ {\rm cm}^2\).
2. megoldás. A következő egyenletrendszer alapján keressük \(\displaystyle ab\)-t:
\(\displaystyle a+b=2\)
\(\displaystyle a^3 + b^3 =5,375.\)
Az elsőből \(\displaystyle a=2-b\), amit a második egyenletbe helyettesítve \(\displaystyle 8-12b+6b^2-b^3 + b^3=5,357\)-t kapunk. \(\displaystyle 6\)-tal való osztás után megoldandó a \(\displaystyle b^2-2b+0,4375=0\) egyenlet, melynek két (diszkrimináns pozitív) megoldása éppen a két kocka élhosszát adja meg. Tudjuk a gyökök és együtthatók közötti összefüggésekből, hogy (főegyüttható \(\displaystyle 1\) lévén) a gyökök szorzata pont a konstans tag. Ezért \(\displaystyle ab=0,4375\). Tehát a fekete téglalap területe \(\displaystyle 0,4375\ {\rm cm}^2\).
Statistics:
332 students sent a solution. 5 points: 296 students. 4 points: 11 students. 3 points: 10 students. 2 points: 5 students. 1 point: 5 students. 0 point: 3 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, January 2010
