 Problem C. 1034. (April 2010)
Problem C. 1034. (April 2010)
C. 1034. A regular hexagon is rotated about its axes of symmetry. Find the ratio of the surface areas of the resulting solids.
(5 pont)
Deadline expired on May 10, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A szabályos hatszögnek kétféle szimmetriatengelye van.
Először tekintsük azt, amelyik két szemközti oldal felezőpontján megy át. Ezen tengely körül forgatva a hatszöget két egybevágó csonkakúp keletkezik. A kérdéses felszín két csonkakúp-palást felszínéből és két kör területéből áll (az alapkör területét nem kell figyelembe venni).
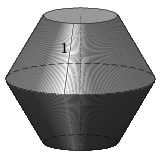
Legyen a hatszög oldala egységnyi, ekkor a fedőkör sugara \(\displaystyle r=\frac{1}{2}\), az alapkör sugara \(\displaystyle R=1\), a csonkakúp alkotója \(\displaystyle a=1\). A fedőkör területe \(\displaystyle \frac{1}{4}\,\pi\), a csonkakúp palást területe \(\displaystyle \frac{3}{2}\,\pi\).
A keresett felszín:
\(\displaystyle F_1=2\cdot \frac{1}{4}\,\pi+ 2\cdot \frac{3}{2}\,\pi= \frac{7}{2}\,\pi. \)
A másik esetben a szimmatriatengely a hatszög két szemközti csúcsán megy át. Ekkor a forgatáskor két egybevágó kúp és egy henger jön létre.
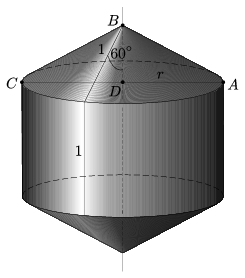
Tekintsük az \(\displaystyle ABC\) egyenlőszárú háromszöget. Az \(\displaystyle AC\) felezőpontja legyen \(\displaystyle D\). A \(\displaystyle BDC\) háromszög egy 1 egység oldalú szabályos háromszög fele, ezért \(\displaystyle r=\frac{\sqrt{3}}{2}\).
A felszín a két kúppalást és a hengerpalást területének összege:
\(\displaystyle T_{\text{kúpok}} = 2r\pi a= 2\cdot \frac{\sqrt{3}}{2}\,\pi\cdot 1= \sqrt{3}\,\pi,\)
\(\displaystyle T_{\text{henger}} = 2r\pi m= \sqrt{3}\, \pi.\)
A két felszín összege \(\displaystyle F_2= 2\sqrt{3}\,\pi\).
A felszínek aránya:
\(\displaystyle \frac{F_1}{F_2}= \frac{\frac{7}{2}\,\pi}{2\sqrt{3}\, \pi}= \frac{7}{4\sqrt{3}}\approx 1{,}0104. \)
A két forgástest felszíne közelítőleg egyenlő.
Keceli-Mészáros Emese (Budapest, Szent István Gimn., 9. évf.)
Statistics:
163 students sent a solution. 5 points: 94 students. 4 points: 21 students. 3 points: 17 students. 2 points: 15 students. 1 point: 11 students. 0 point: 3 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, April 2010
