Problem C. 1035. (May 2010)
Problem C. 1035. (May 2010)
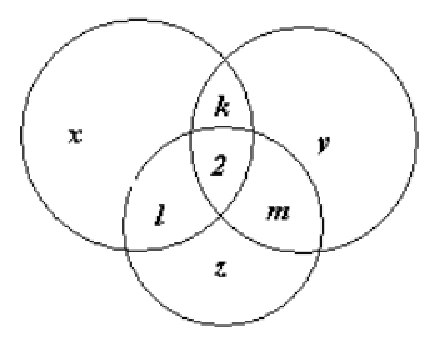
C. 1035. In a mathematics competition, there were three problems. 56 participants solved at least one problem. 2 participants solved all problems. Out of those solving the second problems, 10 more solved the third problem than the first one. The number of those solving both of the first and second problems was 10 larger than the number of those solving the third problem only. All participants solving the first and third problems solved the second problem, too. There were 14 participants altogether who solved the first problem only or the second problem only. How many participants solved the third problem?
(5 pont)
Deadline expired on June 10, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Azok között, akik a másodikat megoldották, 10-zel többen oldották meg a harmadikat, mint az elsőt. Így \(\displaystyle m=l+10\).
Az elsőt és a másodikat is megoldó versenyzők 10-zel többen voltak, mint akik csak a harmadikat oldották meg. Így \(\displaystyle k+2=z+10\).
Aki megoldotta az elsőt és a harmadikat is, az a másodikat is megoldotta. Így \(\displaystyle l=0\).
Akik csak az első, vagy csak a második feladatot oldották meg összesen 14-en voltak. Így \(\displaystyle x+y=14\).
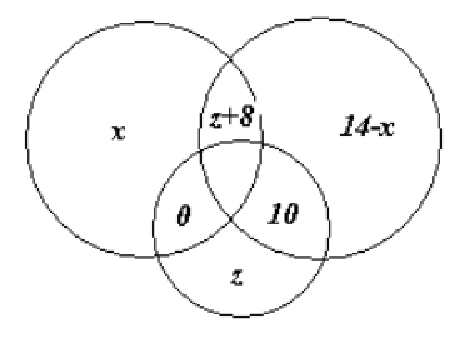
\(\displaystyle x+z+8+14-x+0+2+10+z=56 \qquad \Rightarrow \qquad z=11.\)
Tehát a harmadik feladatot 23-an oldották meg.
|
Statistics:
133 students sent a solution. 5 points: 106 students. 4 points: 10 students. 3 points: 12 students. 2 points: 2 students. 1 point: 1 student. 0 point: 1 student. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, May 2010