 Problem C. 1038. (May 2010)
Problem C. 1038. (May 2010)
C. 1038. Define the function on the set of real numbers as follows:
Solve the equation on the set of real numbers.
(5 pont)
Deadline expired on June 10, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A \(\displaystyle \mathop{\rm lac}\, (x)\) függvény minden \(\displaystyle [2n;2n+1]\) (ahol \(\displaystyle n\in \mathbb{Z}\)) intervallumban megegyezik az \(\displaystyle f(x)=x\) függvénnyel, míg minden egyéb \(\displaystyle \left]2n+1;2n+2\right[\) intervallum képe a \(\displaystyle {g(x)=-x}\) egyenessel párhuzamos, a
\(\displaystyle \left(2n+\frac{3}{2};2n+\frac{3}{2}\right) \)
pontra szimmetrikusan illeszkedő nyílt szakasz (lásd ábra).
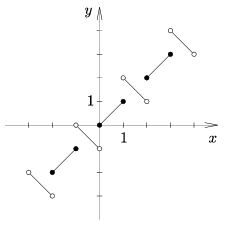
A \(\displaystyle \mathop{\rm lac}\, (x)\) függvény tehát egy kölcsönösen egyértelmű függvény (azaz minden \(\displaystyle x\) értékhez egyetlen \(\displaystyle \mathop{\rm lac}\, (x)\) függvényérték tartozik és fordítva). Ebből a következik, hogy \(\displaystyle \mathop{\rm lac}\, (2x^2+x+4)=\mathop{\rm lac}\, (x^2+7x-1)\) akkor és csak akkor teljesülhet, ha \(\displaystyle 2x^2+x+4=x^2+7x-1\) is teljesül. Az egyenletet rendezve:
\(\displaystyle x^2-6x+5=0. \)
Ebből: \(\displaystyle x_1 =1\), \(\displaystyle x_2 =5\).
Tehát két megoldása van az eredeti egyenletnek.
Neumer Tamás (Budapest, Eötvös József Gimn., 11. évf.)
Statistics:
70 students sent a solution. 5 points: 56 students. 4 points: 1 student. 3 points: 11 students. 1 point: 2 students.
Problems in Mathematics of KöMaL, May 2010
