Problem C. 1044. (September 2010)

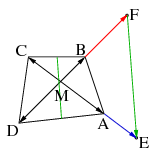
C. 1044. The diagonals of a convex quadrilateral ABCD intersect at point M. Extend diagonal AC beyond A by the length of MC, and extend diagonal BD beyond B by the length of MD to get the points E and F. Prove that EF is parallel to a midline of the quadrilateral.

(5 pont)

Deadline expired on October 11, 2010.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. \(\displaystyle M\)-ből a csúcsokba mutató vektorok legyenek a jelöléseknek megfelelően \(\displaystyle \mathbf a, \mathbf b, \mathbf c, \mathbf d\). Így \(\displaystyle \overrightarrow{ME}=\mathbf a - \mathbf c\) és \(\displaystyle \overrightarrow{MF}=\mathbf b - \mathbf d\), ahonnan \(\displaystyle \overrightarrow{FE}=\mathbf a - \mathbf c - \mathbf b + \mathbf d\). Az \(\displaystyle AD\) szakasz felezőpontjába mutató vektor \(\displaystyle \frac 12(\mathbf a + \mathbf d)\), a \(\displaystyle BC\) szakasz felezőpontjába mutató vektor \(\displaystyle \frac 12(\mathbf b + \mathbf c)\), így az első felezőpontból a másodikba mutató vektor - melynek tartóegyenese a felezőpontok által meghatározott középvonal egyenese - \(\displaystyle \frac 12(\mathbf a + \mathbf d - \mathbf b - \mathbf c)=\frac 12 \overrightarrow{FE}\).

Statistics:

160 students sent a solution.
5 points:	65 students.
4 points:	28 students.
3 points:	10 students.
2 points:	3 students.
1 point:	4 students.
0 point:	32 students.
Unfair, not evaluated:	18 solutionss.

Problems in Mathematics of KöMaL, September 2010