 Problem C. 1049. (October 2010)
Problem C. 1049. (October 2010)
C. 1049. Consider the circles drawn on two adjacent sides of a square of side 2 units. Find the radius of the circle that touches one of the sides and one circle from the inside and the other circle from the outside.
(5 pont)
Deadline expired on November 10, 2010.
Sorry, the solution is available only in Hungarian. Google translation
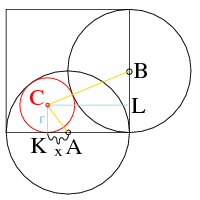
Megoldás. Az egységkörök középpontjai legyenek \(\displaystyle A\) és \(\displaystyle B\), az érintő kör középpontja \(\displaystyle C\), továbbá állítsunk merőlegest mindkét négyzetoldalra \(\displaystyle C\)-ből: a talppontok legyenek \(\displaystyle K\) és \(\displaystyle L\) az ábra szerint. A beírt kör sugara legyen \(\displaystyle r\), \(\displaystyle KA=x\). Az \(\displaystyle ACK\triangle\) és a \(\displaystyle BCL\triangle\) derékszögűek, Pithagorasz tételét felírva mindkét háromszögben \(\displaystyle (1-r)^2=r^2+x^2\) és \(\displaystyle (1+r)^2=(1-r)^2+(1+x)^2\). Az elsőből \(\displaystyle x^2=1-2r\), amit a másodikba helyettesítve rendezés után \(\displaystyle 1-2r+2x+1=4r\), azaz \(\displaystyle x=3r-1\). Az első egyenletből pedig \(\displaystyle x^2=1-2r=9r^2-6r+1\), ahonnan \(\displaystyle 9r^2-4r=0\). Mivel \(\displaystyle r>0\), ezért kapjuk, hogy a beírt kör sugara \(\displaystyle \frac 49\).
Statistics:
173 students sent a solution. 5 points: 106 students. 4 points: 32 students. 3 points: 4 students. 2 points: 3 students. 1 point: 5 students. 0 point: 21 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, October 2010
