 Problem C. 1052. (November 2010)
Problem C. 1052. (November 2010)
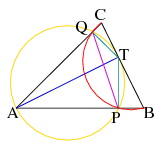
C. 1052. T is the foot of the perpendicular drawn from vertex A of an acute-angled triangle ABC to side BC. The feet of the perpendiculars drawn from T to the sides AB and AC are P and Q. Prove that the quadrilateral BPQC is cyclic.
(5 pont)
Deadline expired on December 10, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Mivel az \(\displaystyle APT\) és \(\displaystyle ATQ\) háromszögek derékszögűek és közös az (\(\displaystyle AT\)) átfogójuk, ezért a köréjük írt (Thalész) kör egybeesik. Úgy is mondhattuk volna, hogy az \(\displaystyle APTQ\) négyszög húrnégyszög, mert a szemközt levő szögeik (feladat szerint \(\displaystyle AT\)-tól különböző félsíkban vannak) összege \(\displaystyle 90^\circ + 90^\circ =180^\circ\). Felhasználva, hogy adott sugarú kör azonos hosszúságú íveihez (v. húrokhoz) tartozó középponti szögek nagysága megegyezik. Így \(\displaystyle TPQ\angle =TAQ\angle = 90^\circ - \gamma\). A vizsgálandó \(\displaystyle BCQP\) négyszögben \(\displaystyle QPB\angle + BCQ\angle = (90^\circ - \gamma + 90^\circ) + \gamma = 180^\circ\), azaz a \(\displaystyle BCPQ\) négyszög húrnégyszög.
Statistics:
181 students sent a solution. 5 points: 101 students. 4 points: 37 students. 3 points: 18 students. 2 points: 10 students. 1 point: 4 students. 0 point: 7 students. Unfair, not evaluated: 4 solutionss.
Problems in Mathematics of KöMaL, November 2010
