Problem C. 1059. (December 2010)

C. 1059. The two diagonals from a vertex of a regular pentagon are drawn. The resulting figure can be folded to form the lateral faces of a pyramid with a regular triangular base. Find the volume of the pyramid.

(5 pont)

Deadline expired on January 10, 2011.

Sorry, the solution is available only in Hungarian. Google translation

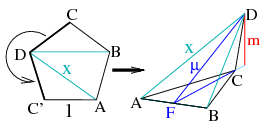
Megoldás. A megoldás során használjuk az ábra jelöléseit. A szabályos ötszöglapból hajtogatható \(\displaystyle ABCD\) gúla alaplapja \(\displaystyle ABC\) háromszög, ami szabályos, egységnyi oldalú. A gúla oldaléleinek hossza \(\displaystyle CD=1\), továbbá \(\displaystyle AD=BD=x\), ahol \(\displaystyle x\) a szabályos ötszög átlójának hossza: \(\displaystyle x=2\sin 54^\circ=\frac{1+\sqrt 5}{2}\approx 1,618\). A gúla szimmetrikus a \(\displaystyle DC\) oldalélen átmenő, az alaplap síkjára merőleges síkra (mely az alaplapot és az \(\displaystyle ABD\) oldallapot is az \(\displaystyle AB\)-hez tartozó oldalfelező merőlegesekben metsz, melyek a magasságegyenesek is egyben). A gúla magassága tehát a \(\displaystyle CDF\) háromszög \(\displaystyle FC\)-hez tartozó magassága. Az \(\displaystyle ABC\) szabályos háromszögben \(\displaystyle FC=\frac{\sqrt 3}{2}\), a \(\displaystyle BDF\) derékszögű háromszögben pedig \(\displaystyle \mu^2=FD^2=x^2-\frac 12=\frac{5+2\sqrt{5}}{4}\). A \(\displaystyle CDF\triangle\)-ben a \(\displaystyle C\)-nél levő szög legyen \(\displaystyle \varphi\). Ekkor a koszinusz-tétel szerint \(\displaystyle \mu^2=\frac 34 + 1-2\cdot \frac{\sqrt3}{2} \cdot \cos \varphi\), ahonnan \(\displaystyle \cos\varphi=\frac{2-2\sqrt 5}{4\sqrt 3}\approx -0,356822\). Az \(\displaystyle FC\)-hez tartozó magasság \(\displaystyle m=1\cdot \sin\varphi=\sqrt{\frac{3+\sqrt 5}6}\approx 0,934172\). A gúla térfogata \(\displaystyle V=\frac 13 t_{ABC}\cdot m=\frac 13 \cdot \frac{\sqrt3}4\cdot\sqrt{\frac{3+\sqrt 5}6}=\frac{\sqrt{6+2\sqrt 5}}{24}=\frac{1+\sqrt 5}{24}\approx 0,1348\).

Statistics:

157 students sent a solution.
5 points:	70 students.
4 points:	27 students.
3 points:	24 students.
2 points:	20 students.
1 point:	9 students.
0 point:	5 students.
Unfair, not evaluated:	2 solutionss.

Problems in Mathematics of KöMaL, December 2010