 Problem C. 1063. (January 2011)
Problem C. 1063. (January 2011)
C. 1063. A vertical wall of a building is a square of side 20 metres. The angles subtended by the vertical sides of the square at two points on the (level) ground are measured. The results are 40o and 38o at one point, and 32o and 40o at the other point. Find the distance between the two points.
(5 pont)
Deadline expired on February 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Készítsünk ábrát. A két észlelési pontot jelöljük \(\displaystyle P_1\)-gyel és \(\displaystyle P_2\)-vel.
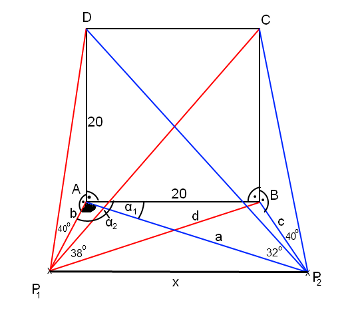
Az \(\displaystyle AP_1D\) háromszögben meg tudjuk határozni a \(\displaystyle b\)-vel jelölt szakasz hosszát: \(\displaystyle \tg 40^{\circ}=\frac{20}{b}\), amiből \(\displaystyle b=\frac{20}{\tg 40^{\circ}}\approx23,835.\) Ezzel a módszerrel sorra meghatározzuk az \(\displaystyle a\), \(\displaystyle c\) és \(\displaystyle d\) szakaszok hosszát.
A \(\displaystyle DAP_2\) háromszögben: \(\displaystyle a=\frac{20}{\tg 32^{\circ}}\approx32,001.\)
A \(\displaystyle CBP_2\) háromszögben: \(\displaystyle c=\frac{20}{\tg 40^{\circ}}\approx23,835.\)
A \(\displaystyle P_1BC\) háromszögben: \(\displaystyle d=\frac{20}{\tg 38^{\circ}}\approx25,599.\)
Ezután olyan háromszögeink keletkeznek, amelyeknek ismerjük mindhárom oldalát és az egyik szögüket szeretnénk kiszámolni. Erre koszinusz-tételeket használunk.
Az \(\displaystyle \alpha _1\)-gyel jelölt szöget az \(\displaystyle ABP_2\) háromszögben felírt koszinusz-tétellel kapjuk meg:
\(\displaystyle c^2=a^2+20^2-2a\cdot 20\cos \alpha _1,\)
\(\displaystyle \alpha _1\approx48,034^{\circ}.\)
Az \(\displaystyle \alpha _2\)-vel jelölt szöget az \(\displaystyle AP_1B\) háromszögben felírt koszinusz-tétellel kapjuk meg:
\(\displaystyle d^2=b^2+20^2-2 b\cdot 20 \cos \alpha _2,\)
amiből \(\displaystyle \alpha _2\approx70,847^{\circ}.\)
A két észlelési pont távolságát \(\displaystyle x\)-szel jelöltem. \(\displaystyle x\)-et is egy koszinusz-tétellel tudjuk kiszámolni, de előbb meg kell határoznunk az ábrán feketével jelölt szöget. A szög nagysága: \(\displaystyle \alpha _2-\alpha _1=22,813^{\circ}.\)
Most már meg tudjuk határozni \(\displaystyle x\)-et a \(\displaystyle P_1AP_2\) háromszögben felírt koszinusz-tétellel:
\(\displaystyle x^2=b^2+a^2-2b\cos 22,813^{\circ}.\)
Ebből \(\displaystyle x\)-re 13,639-et kapunk.
Tehát a két észlelési pont távolsága 13,639 méter.
Enyedi Péter (Szekszárd, Garay János Gimn., 11. o. t.)
Statistics:
121 students sent a solution. 5 points: 76 students. 3 points: 2 students. 2 points: 20 students. 1 point: 13 students. 0 point: 6 students. Unfair, not evaluated: 4 solutionss.
Problems in Mathematics of KöMaL, January 2011
