 Problem C. 1068. (February 2011)
Problem C. 1068. (February 2011)
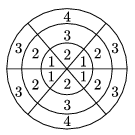
C. 1068. A target consists of 18 fields bounded by three concentric circles and three line segments through the centre, as shown in the figure. The areas of the fields marked with the same number are equal, and the area of number 2 is half that of number 3. By what factor is number 4 greater in area than number 1?
(5 pont)
Deadline expired on March 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A körök sugara legyen \(\displaystyle \varrho < r < R\) az 1. körcikk szöge (ívmértékben) \(\displaystyle \alpha\). A területek: \(\displaystyle t_1=1/2\alpha\varrho^2\), \(\displaystyle t_2=1/2(\pi - 2\alpha)\varrho^2=1/2\alpha(r^2 - \varrho^2)\), \(\displaystyle t_3=1/2 \alpha(R^2-r^2)=1/2(\pi - 2\alpha)(r^2 - \varrho^2)\), ahonnan \(\displaystyle R^2=\frac{\pi - 2\alpha}{\alpha}(r^2-\varrho^2)+r^2=\). Mivel \(\displaystyle 2t_2=t_3\), ezért -a középső körgyűrűbeli részek összehasonlításából- \(\displaystyle \pi -2\alpha=\alpha\) (azaz \(\displaystyle \alpha=\frac\pi3\)). Végül \(\displaystyle t_4=1/2(\pi - 2\alpha)(R^2-r^2)= 1/2\frac{(\pi - 2\alpha)^2}{\alpha}(r^2 - \varrho^2)=1/2\frac{(\pi - 2\alpha)^3}{\alpha^2}\varrho^2=1/2\frac{8\alpha^3}{\alpha^3}\alpha \varrho^2=8t_1\). A 4-es mező területe nyolcszorosa az 1-es mező területének.
Statistics:
191 students sent a solution. 5 points: 103 students. 4 points: 36 students. 3 points: 26 students. 2 points: 14 students. 1 point: 5 students. 0 point: 3 students. Unfair, not evaluated: 4 solutionss.
Problems in Mathematics of KöMaL, February 2011
