Problem C. 1077.

Order KöMaL!

ELTE

Competitions Portal

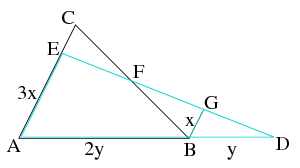
C. 1077. E is the point dividing side AC of triangle ABC in a 3:1 ratio, such that EC is the shorter part. The line passing through E and the midpoint F of side BC intersects the line AB at D. What percentage is the area of triangle ADE of the triangle ABC?

(5 points)

Deadline expired.

Sorry, the solution is published in Hungarian only.

A háromszög B csúcsából húzzunk párhuzamost az AC oldallal: ez G-ben metszi ED-t. $FBG_\triangle \cong FCE_\triangle$ , mert a párhuzamos oldalaik miatt hasonlóak és F felezőpont miatt CF=FB (azaz F-re középpontosan tükrösek), így BG=EC=AC/4=x (és AE=3x). $ADE_\triangle \sim BDG_\triangle$ az egyállású szögeik miatt, így az oldalakra $\frac{x}{3x}=\frac{GB}{EA}=\frac{BD}{AD}=\frac{y}{3y}$ , azaz AB=2y. A területek aránya pedig

$\frac{t_{ADE}}{t_{ABC}}=\frac{{1 \over 2}AE\cdot AD\cdot \sin\alpha}{{1 \over 2}AC\cdot AB\cdot \sin\alpha}=\frac{9xy}{8xy}=\frac 98 .$

Az ADE háromszög területe 112,5%-a az ABC háromszög területének.

Statistics on problem C. 1077.

117 students sent a solution.

5 points: 103 students.

4 points: 7 students.

3 points: 2 students.

2 points: 1 student.

0 point: 4 students.

Problems in Mathematics of KöMaL, April 2011

Our web pages are supported by:

ELTE