Problem C. 1079. (April 2011)

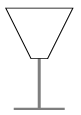
C. 1079. We have a champagne glass shaped like a truncated cone. The radius of the base circle is 1 cm, the radius of the top circle is 4 cm and its height is 6 cm (see the figure). To what height do we need to fill the glass to have half a glass of drink?

(5 pont)

Deadline expired on May 10, 2011.

Sorry, the solution is available only in Hungarian. Google translation

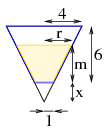
Megoldás. Egészítsük ki a poharat adó csonkakúpot kúppá, ennek keresztmetszete látható az ábrán. A csonkakúpot kúppá egy olyan kúppal egészítettük ki, mely alapkörének sugara 1cm, magassága \(\displaystyle x\), térfogatát jelöljük \(\displaystyle V_1\)-gyel. Töltsük \(\displaystyle m\) magasságig a poharat pezsgővel. A kiegészítő kúp és a poharat tartalmazó kúp hasonlóak, a hasonlóság aránya 1:4, így a magasságaikra \(\displaystyle x:(6+x)=1:4\), ahonnan \(\displaystyle x=2\)(cm); a pezsgővel töltött pohárrészre a (kúpok) hasonlóságból pedig \(\displaystyle r:1=(m+2):2\). A pohár űrtartalma \(\displaystyle V_0=\frac 13 \pi(4^2\cdot 8-1^2 \cdot 2)=42\pi (cm^3)\). A feladat szerint \(\displaystyle 21\pi (cm^3)\) pezsgőt töltöttünk: \(\displaystyle 21\pi (cm^3)=\frac 13 \pi \left((\frac{m+2}2)^2 \cdot (m+2) -1^2 \cdot 2\right)\), ahonnan \(\displaystyle m\approx 4,38\)(cm).

Statistics:

135 students sent a solution.
5 points:	78 students.
4 points:	25 students.
3 points:	7 students.
2 points:	17 students.
1 point:	6 students.
0 point:	1 student.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, April 2011