 Problem C. 1083. (May 2011)
Problem C. 1083. (May 2011)
C. 1083. The length of one side of a triangle is 8 cm, one of the angles lying on it is 60o, and the radius of the inscribed circle is cm. How long are the other two sides?
(5 pont)
Deadline expired on June 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás.
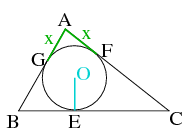
Az \(\displaystyle ABC\) háromszög beírt köre az oldalakat az \(\displaystyle E\), \(\displaystyle F\) és \(\displaystyle G\) pontokban érinti. A \(\displaystyle BEO\) derékszögű háromszög egyik befogója \(\displaystyle \sqrt 3\) hosszú, a vele szemközti szög pedig \(\displaystyle 30^\circ\), ezért \(\displaystyle BE=\sqrt 3 \cdot \ctg 30^\circ =3=BG\). Az \(\displaystyle ABC\) háromszög területének kétszerese a beírt kör sugarának segítségével \(\displaystyle 2t=(8+CF+x+x+GB)\cdot \sqrt 3 =(16+2x)\cdot \sqrt 3\), másrészről két oldalának és a közrezárt szög segítségével \(\displaystyle 2t=8(3+x)\cdot \sin 60^\circ.\) E kettő egyenlőségéből \(\displaystyle 16+2x=4(3+x)\), ahonnan \(\displaystyle x=2\). A háromszög oldalai tehát \(\displaystyle AB=3+2=5\)cm és \(\displaystyle CA=8-3+2=7\)cm.
Statistics:
101 students sent a solution. 5 points: 55 students. 4 points: 2 students. 3 points: 38 students. 2 points: 2 students. Unfair, not evaluated: 4 solutionss.
Problems in Mathematics of KöMaL, May 2011
