 Problem C. 1099. (November 2011)
Problem C. 1099. (November 2011)
C. 1099. In a quadrilateral ABCD, M is the midpoint of line segment AB, and N is the midpoint of line segment CD. The length of diagonals AC and BD is , and they enclose an angle of 60o. Find the distance MN.
Suggested by G. Dávid, Matlap, Kolozsvár
(5 pont)
Deadline expired on December 12, 2011.
Sorry, the solution is available only in Hungarian. Google translation
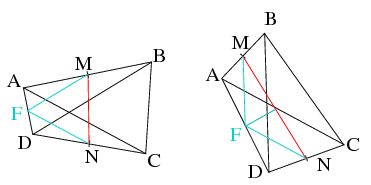
Megoldás. Használjuk az ábra jelöléseit, az \(\displaystyle F\) az \(\displaystyle AD\) felezőpontja. Az első esetben \(\displaystyle FM\) középvonal \(\displaystyle ADB\) háromszögben és \(\displaystyle FN\) középvonal \(\displaystyle ADC\) háromszögben, ezért \(\displaystyle FM=FN=\sqrt3\), továbbá bezért szögük \(\displaystyle 60^\circ\). Tehát \(\displaystyle MFN\) háromszög szabályos, ezért \(\displaystyle MN=\sqrt3\).
A második esetben \(\displaystyle MFN\) háromszög egyenlőszárú, a szárszöge \(\displaystyle 120^\circ\). \(\displaystyle MN\) hossza koszinusz-tétellel számolható, vagy az első eset szabályos háromszögének magasságának kétszereseként: \(\displaystyle 2\cdot\frac{\sqrt3}2\cdot \sqrt3\), azaz \(\displaystyle MN=3\).
Statistics:
246 students sent a solution. 5 points: 59 students. 4 points: 5 students. 3 points: 103 students. 2 points: 17 students. 1 point: 29 students. 0 point: 27 students. Unfair, not evaluated: 6 solutionss.
Problems in Mathematics of KöMaL, November 2011
