 |
A C. 1099. feladat (2011. november) |
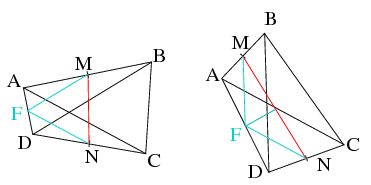
C. 1099. Az ABCD négyszögben M az AB, N pedig a CD szakasz felezőpontja. Az AC és BD átlók hossza , és 60o-os szöget zárnak be. Mekkora az MN szakasz?
Javasolta: Dávid Géza (Matlap, Kolozsvár)
(5 pont)
A beküldési határidő 2011. december 12-én LEJÁRT.
Megoldás. Használjuk az ábra jelöléseit, az \(\displaystyle F\) az \(\displaystyle AD\) felezőpontja. Az első esetben \(\displaystyle FM\) középvonal \(\displaystyle ADB\) háromszögben és \(\displaystyle FN\) középvonal \(\displaystyle ADC\) háromszögben, ezért \(\displaystyle FM=FN=\sqrt3\), továbbá bezért szögük \(\displaystyle 60^\circ\). Tehát \(\displaystyle MFN\) háromszög szabályos, ezért \(\displaystyle MN=\sqrt3\).
A második esetben \(\displaystyle MFN\) háromszög egyenlőszárú, a szárszöge \(\displaystyle 120^\circ\). \(\displaystyle MN\) hossza koszinusz-tétellel számolható, vagy az első eset szabályos háromszögének magasságának kétszereseként: \(\displaystyle 2\cdot\frac{\sqrt3}2\cdot \sqrt3\), azaz \(\displaystyle MN=3\).
Statisztika:
246 dolgozat érkezett. 5 pontot kapott: 59 versenyző. 4 pontot kapott: 5 versenyző. 3 pontot kapott: 103 versenyző. 2 pontot kapott: 17 versenyző. 1 pontot kapott: 29 versenyző. 0 pontot kapott: 27 versenyző. Nem versenyszerű: 6 dolgozat.
A KöMaL 2011. novemberi matematika feladatai

