 Problem C. 1102. (December 2011)
Problem C. 1102. (December 2011)
C. 1102. D is the foot of the altitude drawn from vertex C of an acute-angled triangle ABC. Construct that line parallel to AB whose segment inside the triangle subtends a right angle at D.
(Suggested by G. Holló, Budapest)
(5 pont)
Deadline expired on January 10, 2012.
Sorry, the solution is available only in Hungarian. Google translation
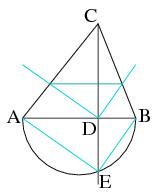
Megoldás. Szerkesszünk \(\displaystyle AB\) fölé Thalesz-kört: a \(\displaystyle C\)-n átmenő magasságegyenest a háromszögön kívül metsze \(\displaystyle E\)-ben. Az \(\displaystyle EAB\) háromszöget középpontosan kicsinyítsük le \(\displaystyle C\)-ből úgy, hogy \(\displaystyle E\) képe \(\displaystyle D\) legyen, azaz \(\displaystyle D\)-n keresztül szerkesszünk párhuzamost \(\displaystyle AE\) és \(\displaystyle BE\) szakaszok egyenesével. Ezen párhuzamosok metszéspontját rendre \(\displaystyle AC\)-vel és \(\displaystyle BC\)-vel összekötve kapjuk azt az \(\displaystyle AB\)-vel párhuzamos szakaszt, mely \(\displaystyle D\)-ből derékszög alatt látszik.
Mivel \(\displaystyle ABC\) hegyesszögű, ezért \(\displaystyle D\) az \(\displaystyle AB\) belsejébe esik, a szerkesztett metszéspontok egyértelműen (és mindig) léteznek.
Statistics:
191 students sent a solution. 5 points: 73 students. 4 points: 56 students. 3 points: 24 students. 2 points: 3 students. 1 point: 6 students. 0 point: 25 students. Unfair, not evaluated: 4 solutionss.
Problems in Mathematics of KöMaL, December 2011
