Problem C. 1106. (January 2012)

C. 1106. Depending on the parameter a, how many zeros does the function defined by

$f(x)= \left\{ \matrix{ \sqrt{x^2 + 4x +4}-a, & {\rm if\ } x\le 0,\cr x^2-4x+a, & {\rm if\ } x>0 \cr }\right.$

have?

(5 pont)

Deadline expired on February 10, 2012.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás.

$\displaystyle \sqrt{x^2 + 4x +4}-a=\sqrt{(x+2)^2}-a=|x+2|-a=$

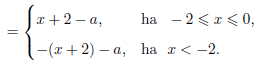
$\displaystyle x^2-4x+a=(x-2)^2-4+a$, ha $\displaystyle x>0$.

Tehát

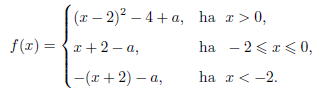
Ábrázoljuk a függvényt $\displaystyle a=0$ esetén:

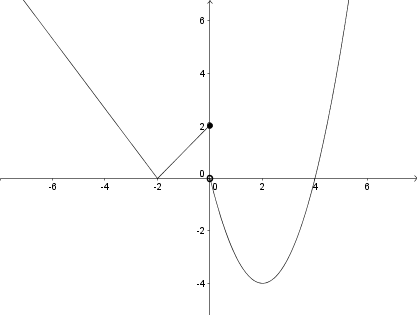
Nézzük meg $\displaystyle f(x)$ zérushelyeinek számát $\displaystyle a$ paramétertől függően az $\displaystyle x\leq0$, illetve az $\displaystyle x>0$ intervallumon.

A függvény képe az $\displaystyle x\leq0$ intervallumon $\displaystyle a$ paraméterrel az $\displaystyle y$ tengely mentén lefelé, míg az $\displaystyle x>0$ intervallumon $\displaystyle a$ paraméterrel felfelé tolódik.

$\displaystyle a$ értéke	zérushelyek száma az $\displaystyle x\leq0$ intervallumon
$\displaystyle a<0$	$\displaystyle 0$
$\displaystyle a=0$	1
$\displaystyle 0<a\leq2$	2
$\displaystyle a>2$	1

$\displaystyle a$ értéke	zérushelyek száma az $\displaystyle x>0$ intervallumon
$\displaystyle a\leq0$	$\displaystyle 1$
$\displaystyle 0<a<4$	2
$\displaystyle a=4$	1
$\displaystyle a>4$	0

A két táblázat alapján a zérushelyek száma $\displaystyle a$ paramétertől függően:

$\displaystyle a$ értéke	zérushelyek száma az $\displaystyle x>0$ intervallumon
$\displaystyle a\leq0$	$\displaystyle 1$
$\displaystyle a=0$	$\displaystyle 2$
$\displaystyle 0<a\leq2$	4
$\displaystyle 2<a<4$	3
$\displaystyle a=4$	2
$\displaystyle a>4$	1

Rónai Máté (Kőszeg, Jurisich Miklós Gimn., 11. o. t.)

Statistics:

274 students sent a solution.

5 points: 169 students.

4 points: 46 students.

3 points: 33 students.

2 points: 9 students.

1 point: 8 students.

0 point: 5 students.

Unfair, not evaluated: 4 solutionss.

Problems in Mathematics of KöMaL, January 2012

274 students sent a solution.
5 points:	169 students.
4 points:	46 students.
3 points:	33 students.
2 points:	9 students.
1 point:	8 students.
0 point:	5 students.
Unfair, not evaluated:	4 solutionss.

Already signed up?
New to KöMaL?