 Problem C. 1113. (February 2012)
Problem C. 1113. (February 2012)
C. 1113. P is the point in the interior of a rectangle ABCD for which the tangents of the angles  PAB,
PAB,  PBC,
PBC,  PCD and
PCD and  PDA are 1, 2,
PDA are 1, 2, and
, respectively. What is the tangent of the angle enclosed by the diagonals?
(5 pont)
Deadline expired on March 12, 2012.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Használjuk az ábra jelöléseit: a \(\displaystyle P\) pont merőleges vetülete az \(\displaystyle AB\), \(\displaystyle BC\), \(\displaystyle CD\), illetve \(\displaystyle DA\) oldalakra legyen rendre \(\displaystyle E\), \(\displaystyle F\), \(\displaystyle G\) és \(\displaystyle H\). Mivel \(\displaystyle ABCD\) téglalap, ezért \(\displaystyle PFCG\), \(\displaystyle HPGD\), \(\displaystyle AEPH\) és \(\displaystyle EBFP\) is téglalapok (három szögük derékszög), és így \(\displaystyle EB=PF=GC\), \(\displaystyle AE=HP=DG\), \(\displaystyle AH=EP=BF\) és \(\displaystyle HD=PG=FC\).
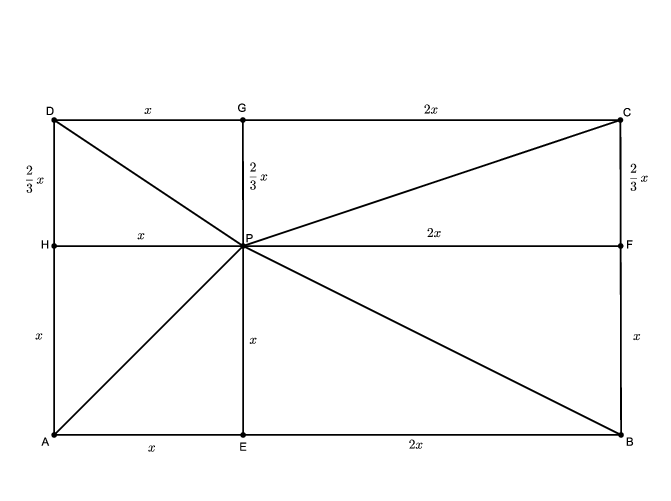
Jelölje az \(\displaystyle AE\) szakasz hosszát \(\displaystyle x\), ekkor \(\displaystyle HP=DG=x\). Mivel \(\displaystyle 1=\tg PAB\sphericalangle=\tg PAE\sphericalangle=\frac{PE}{AE}\), ezért \(\displaystyle PE=x\), amiből \(\displaystyle AH=BF=x\). Mivel \(\displaystyle 2=\tg PBC\sphericalangle=\tg PBF\sphericalangle=\frac{PF}{BF}\), ezért \(\displaystyle PF=2x\), és így \(\displaystyle EB=GC=2x\). Hasonlóan, az \(\displaystyle \frac13=\tg PCD\sphericalangle=\tg PCG\sphericalangle=\frac{PG}{GC}\) egyenlőségből \(\displaystyle PG=\frac23x\) és így \(\displaystyle HD=FC=\frac23x\) következik. Ekkor pedig \(\displaystyle \tg PDA\sphericalangle=\tg PDH\sphericalangle=\frac{PH}{HD}=\frac{x}{\frac23x}=\frac32\) teljesül.
A téglalap oldalainak hossza: \(\displaystyle AB=x+2x=3x\) és \(\displaystyle BC=x+\frac23x=\frac53x\).
Ezek alapján az átlók szögének tangensét már könnyen kiszámíthatjuk. Az átlók metszéspontját jelölje \(\displaystyle M\), az \(\displaystyle M\) merőleges vetületét a \(\displaystyle BC\) oldalra \(\displaystyle N\), az \(\displaystyle NMC\) szöget pedig \(\displaystyle \varphi\). A szimmetria miatt ekkor az átlók által bezárt szög \(\displaystyle 2\varphi\).
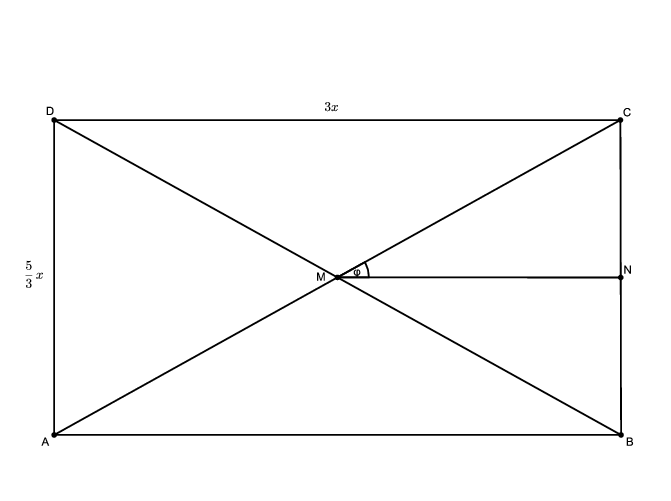
Tudjuk, hogy \(\displaystyle \tg\varphi=\tg NMC\sphericalangle=\frac{CN}{MN}=\frac{\frac12\cdot\frac53x}{\frac12\cdot3x}=\frac59\). A szögek kétszeresének tangensére vonatkozó összefüggés felhasználásával:
\(\displaystyle \tg BMC\sphericalangle=\tg2\varphi=\frac{2\tg\varphi}{1-\tg^2\varphi}=\frac{2\cdot\frac59}{1-\left(\frac59\right)^2}=\frac{\frac{10}{9}}{1-\frac{25}{81}}= \frac{\frac{10}{9}}{\frac{81-25}{81}}=\frac{\frac{90}{81}}{\frac{56}{81}}=\frac{45}{28}.\)
Statistics:
190 students sent a solution. 5 points: 104 students. 4 points: 46 students. 3 points: 23 students. 2 points: 6 students. 1 point: 4 students. 0 point: 1 student. Unfair, not evaluated: 6 solutionss.
Problems in Mathematics of KöMaL, February 2012
