Problem C. 1122. (April 2012)

C. 1122. The angle bisector of angle BAC of a triangle ABC intersects side BC at A₁. Let the centres of the circumscribed circles of triangles ABC, ABA₁, ACA₁ be O, O₁, O₂, respectively. Prove that triangle OO₁O₂ is isosceles.

(5 pont)

Deadline expired on May 10, 2012.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az AB, az AC és az AA₁ szakaszok felezőmerőlegeseit behúzva, a megfelelők metszéspontjaként megkapjuk a körök középpontjait.

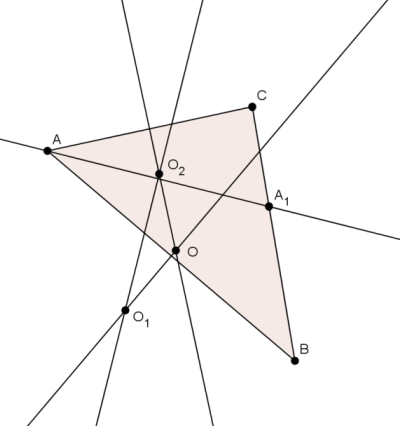
O₁O₂O és CAO₂ merőleges szárú hegyesszögek, így egyenlők.

O₂O₁O és BAO₂ szintén merőleges szárú hegyesszögek, ezért egyenlők.

CAO₂=BAO₂, mert AA₁ szögfelező.

A fentiek miatt O₁O₂O=O₂O₁O, és így az OO₁O₂ háromszög egyenlő szárú.

Statistics:

113 students sent a solution.
5 points:	106 students.
4 points:	5 students.
0 point:	2 students.

Problems in Mathematics of KöMaL, April 2012