 |
A C. 1126. feladat (2012. május) |
C. 1126. A 30 cm sugarú, O1 középpontú kör egyik átmérője AB. Ezt a kört belülről érinti az O2 középpontú, 15 cm sugarú kör az A-ban, valamint az O3 középpontú, 10 cm sugarú kör a B-ben. Mekkora azoknak a köröknek a sugara, amelyek mindhárom kört érintik?
(5 pont)
A beküldési határidő 2012. június 11-én LEJÁRT.
Megoldás. Négy ilyen kör van.
Ebből kettőnek a középpontja az \(\displaystyle AB\) szakaszon van.
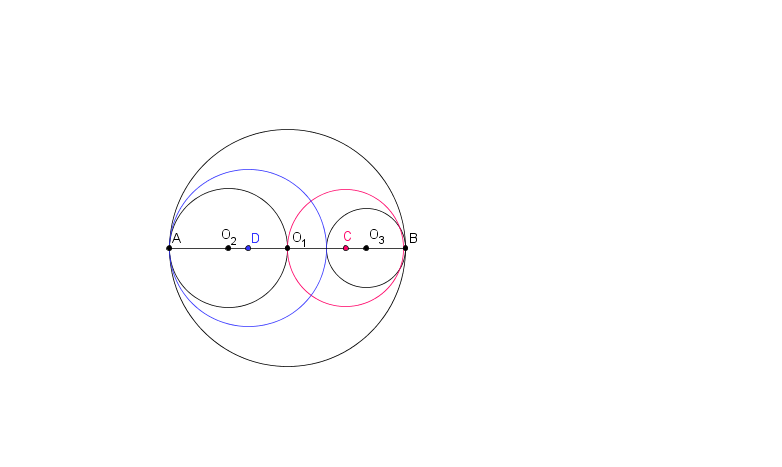
A \(\displaystyle C\) középpontú, piros kör sugara az \(\displaystyle O_1B\) szakasz fele, vagyis 15 cm. A \(\displaystyle D\) középpontú, kék kör átmérője \(\displaystyle 60-20=40\), így sugara 20 cm.
A másik két kör az \(\displaystyle AB\) egyenesére szimmetrikusan helyezkedik el. Elég az egyiket vizsgálni.
Készítsünk ábrát. Legyen a kör középpontja \(\displaystyle K\), a \(\displaystyle K\)-ból az \(\displaystyle O_1O_3\) szakaszra állított merőleges talppontja \(\displaystyle M\), az \(\displaystyle O_1M\) szakasz hossza pedig \(\displaystyle x\).
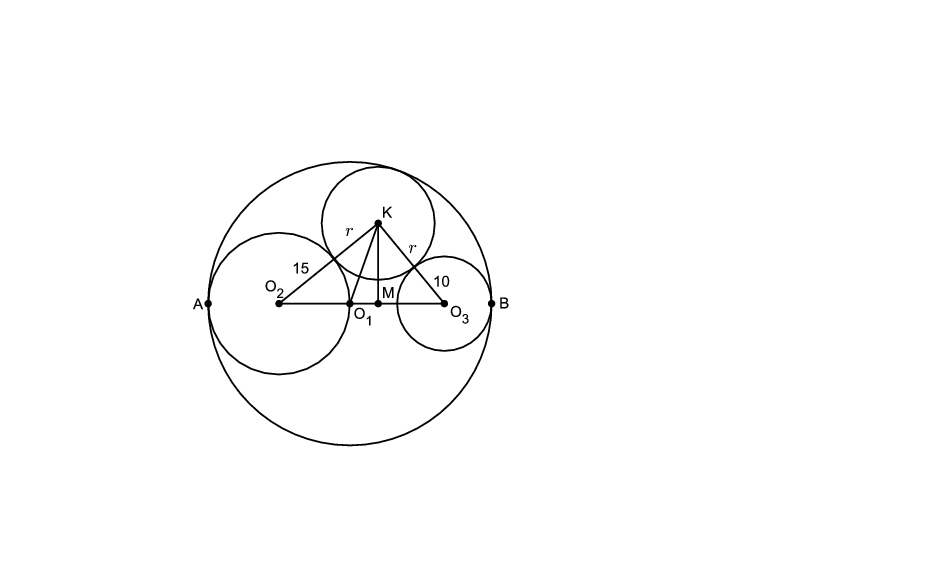
Írjunk fel a Pitagorasz-tételt az \(\displaystyle O_2MK\), az \(\displaystyle O_1MK\) és az \(\displaystyle MO_3K\) háromszögekre.
\(\displaystyle (15+x)^2+m^2=(r+15)^2,\)
\(\displaystyle x^2+m^2=(30-r)^2,\)
\(\displaystyle (20-x)^2+m^2=(r+10)^2.\)
A második egyenletet a másik kettőből kivonva, majd rendezve a kapott két egyenletet:
\(\displaystyle x=3r-30,\)
\(\displaystyle x=-2r+30.\)
Innen \(\displaystyle r=12\) cm (és \(\displaystyle x=6\) cm).
Statisztika:
112 dolgozat érkezett. 5 pontot kapott: Almási Péter, Buttinger Milán, Csibi Levente, Déri Tamás, Fehér Zsuzsanna, Fekete Panna, Gnandt Balázs, Gyurcsik Dóra, Holczer András, Károly Péter Balázs, Katona 100 Bálint, Mezősi Máté, Mócsy Márk, Móricz Tamás, Németh Klára Anna, Pacheco Ana Esther, Papp Gergely, Prokaj Dániel, Qian Lívia, Rácz 413 Bence, Sándor Krisztián, Sárvári Péter, Simkó Irén, Soós Tamás Sándor, Straubinger Dániel, Szaksz Bence, Tamás Kristóf, Temesvári Fanni, Tilk Bence, Tóth 120 Krisztián, Trócsányi Péter, Vargha Sára, Vesztergombi Tamás. 4 pontot kapott: 59 versenyző. 3 pontot kapott: 9 versenyző. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2012. májusi matematika feladatai

