Problem C. 1134. (September 2012)

C. 1134. One base of an isosceles trapezium is three times the height, and the other base is two times the height. With a line parallel to one leg, the trapezium is divided into a parallelogram and an isosceles triangle. The diagonals of the trapezium and of the parallelogram are drawn. Prove that the area of the triangle bounded by the diagonals is 1/25 of the area of the trapezium.

(5 pont)

Deadline expired on October 10, 2012.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Jelölje a trapéz magasságát m. Használjuk az ábra jelöléseit.

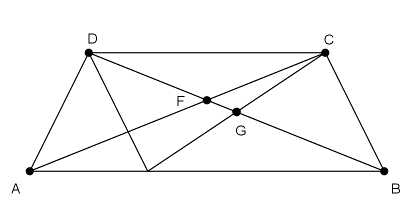
A trapéz területe $\frac{(2m+3m)\cdot m}{2}=\frac{5m^2}{2}$ .

t_FGC=t_DCG-t_DCF.

A paralelogramma átlói felezik egymást, ezért a DCG háromszög magassága m/2:

$t_{DCG}=\frac{2m\cdot\frac m2}{2}=\frac{m^2}{2}.$

A DCF és az ABF háromszögek hasonlók, a hasonlósági arány pedig 2:3. Így a magasságaik aránya is 2:3, vagyis a DCF háromszög magassága $\frac25m$ .

Így

$t_{DCF}=\frac{2m\cdot\frac25m}{2}=\frac25m^2.$

Tehát

$t_{FGC}=\frac{m^2}{2}-\frac25m^2=\frac{m^2}{10}=\frac{1}{25}\cdot\frac{5m^2}{2}.$

Megjegyzés. A feladat állítása igaz, ha az egyik alap 3/2-szerese a másik alapnak, és a magasság tetszőleges.

Statistics:

318 students sent a solution.

5 points: 252 students.

4 points: 41 students.

3 points: 10 students.

1 point: 9 students.

0 point: 4 students.

Unfair, not evaluated: 2 solutionss.

Problems in Mathematics of KöMaL, September 2012

318 students sent a solution.
5 points:	252 students.
4 points:	41 students.
3 points:	10 students.
1 point:	9 students.
0 point:	4 students.
Unfair, not evaluated:	2 solutionss.

Already signed up?
New to KöMaL?