 Problem C. 1148. (December 2012)
Problem C. 1148. (December 2012)
C. 1148. The diagonals of a quadrilateral inscribed in a circle are perpendicular. Prove that the distance of any side from the centre of the circle is equal to the half of the opposite side.
Kvant
(5 pont)
Deadline expired on January 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Készítsünk ábrát.
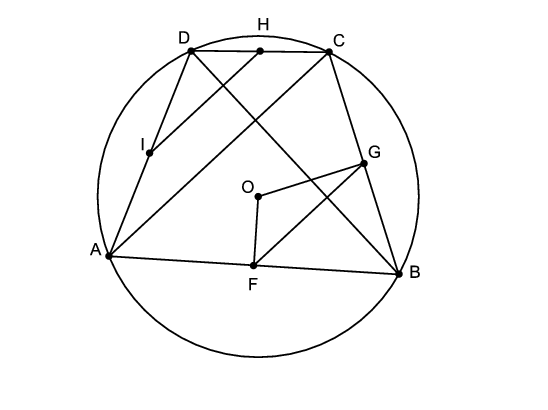
Kössük össze egymással az \(\displaystyle F\), \(\displaystyle G\) és \(\displaystyle H\), \(\displaystyle I\) oldalfelező pontokat. Az \(\displaystyle FG\), illetve \(\displaystyle HI\) szakaszok az \(\displaystyle ABC\), illetve az \(\displaystyle ACD\) részháromszögekben középvonalak, így az \(\displaystyle AC\) átló felével, és így egymással is egyenlők.
Könnyen belátható, hogy \(\displaystyle DIH\angle=DAC\angle=OGF\angle\), illetve \(\displaystyle DHI\angle=DCA\angle=OFG\angle\):
\(\displaystyle DIH\angle=DAC\angle\) és \(\displaystyle DHI\angle=DCA\angle\), mert egyállású szögek. \(\displaystyle DAC\angle=DBC\angle\) a kerületi szögek tétele miatt, \(\displaystyle DBC\angle=OGF\angle\), mert merőleges szárú szögek (hiszen \(\displaystyle FG\parallel AC\), és \(\displaystyle AC\perp DB\), illetve egy kör középpontját egy húr felezőpontjával összekötő szakasz merőleges a húrra). Hasonlóan \(\displaystyle DCA\angle=DBA\angle\) és \(\displaystyle DBA\angle=OFG\angle\).
Ezekből már következik, hogy az \(\displaystyle OFG\triangle\) és a \(\displaystyle DHI\triangle\) egybevágó, tehát \(\displaystyle OF=DH=\frac{DC}{2}\).
A másik három oldalra ugyanígy lehet belátni az állítást.
Statistics:
169 students sent a solution. 5 points: 127 students. 4 points: 6 students. 3 points: 7 students. 2 points: 2 students. 1 point: 22 students. 0 point: 4 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, December 2012
