 Problem C. 1156. (February 2013)
Problem C. 1156. (February 2013)
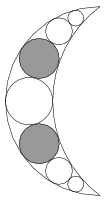
C. 1156. The diagram shows a sketch of a crescent-shaped pendant with line symmetry. The crescent is bounded by a semicircle of radius 20 mm and another circular arc of radius 25 mm. Determine the radius of the shaded circles.
(5 pont)
Deadline expired on March 11, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Tekintsük az alábbi ábrát. Legyen 1 egység 5 mm, mert úgy egyszerűbb lesz a számolás.
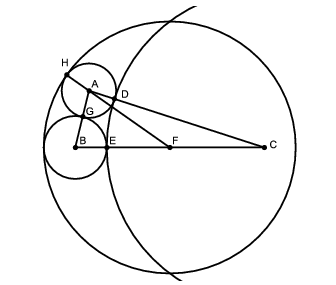
A feladat az \(\displaystyle A\) középpontú kör \(\displaystyle r\) sugarát kérdezi. Mivel \(\displaystyle D\) az \(\displaystyle A\) és a \(\displaystyle C\) sugarú körök érintési pontja, azért \(\displaystyle AD=r\) és \(\displaystyle DC=5\). Mivel \(\displaystyle E\) a \(\displaystyle B\) és a \(\displaystyle C\) középpontú körök érintési pontja, azért \(\displaystyle BE=1\) és \(\displaystyle EF=4-2\cdot1=2\). Innen \(\displaystyle FC=EC-2=5-2=3\). Végül \(\displaystyle H\) az \(\displaystyle A\) és az \(\displaystyle F\) középpontú körök érintési pontja, azért \(\displaystyle HA=r\) és így \(\displaystyle AF=HF-r=4-r\).
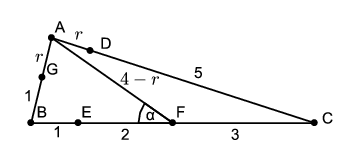
Írjuk fel a koszinusztételt az \(\displaystyle ABF\) háromszögre, majd fejezzük ki \(\displaystyle \cos\alpha\)-t:
\(\displaystyle (1+r)^2=(4-r)^2+3^2-2\cdot(4-r)\cdot3\cos\alpha,\)
| (1) | \(\displaystyle \cos\alpha=\frac{(4-r)^2+3^2-(1+r)^2}{6(4-r)}.\) |
Írjuk fel a koszinusztételt az \(\displaystyle AFC\) háromszögre:
\(\displaystyle (5+r)^2=(4-r)^2+3^2+2\cdot(4-r)\cdot3\cos\alpha.\)
Ebből is kifejezhető \(\displaystyle \cos\alpha\):
| (2) | \(\displaystyle \cos\alpha=\frac{(5+r)^2-(4-r)^2-9}{6(4-r)}.\) |
Mivel (1) és (2) bal oldala megegyezik, ezért jobb oldaluk is egyenlő. Ezt felírva, majd az egyenletet rendezve:
\(\displaystyle \frac{(4-r)^2+3^2-(1+r)^2}{6(4-r)}=\frac{(5+r)^2-(4-r)^2-9}{6(4-r)},\)
\(\displaystyle 16+r^2-8r+9-1-r^2-2r=25+r^2+10r-16-r^2+8r-9,\)
\(\displaystyle 24=28r,\)
\(\displaystyle r=\frac{24}{28}=\frac67.\)
Mivel 1 egység 5 mm, így a kérdéses kör sugara \(\displaystyle \frac{30}{7}\) mm.
Statistics:
104 students sent a solution. 5 points: 58 students. 4 points: 9 students. 3 points: 9 students. 2 points: 6 students. 1 point: 13 students. 0 point: 9 students.
Problems in Mathematics of KöMaL, February 2013
