 Problem C. 1158. (February 2013)
Problem C. 1158. (February 2013)
C. 1158. A kite-shaped plot of land has three interior angles of 80o. Its area is 900 m2. What length of fencing is needed around the whole plot?
(5 pont)
Deadline expired on March 11, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Ha behúzzuk azt az átlót, amelyik nem a szimmetriatengelyen van, akkor a telekből levágunk egy olyan egyenlő szárú háromszöget, malynek a szárszöge \(\displaystyle 80^{\circ}\)-os, így alapon fekvő szögei \(\displaystyle 50^{\circ}\)-osak; és egy olyat, aminek szárszöge \(\displaystyle 120^{\circ}\), alapon fekvő szögei pedig \(\displaystyle 30^{\circ}\) fokosak.
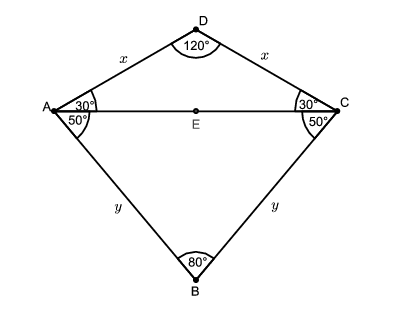
Fejezzük ki a telek területét \(\displaystyle x\) segítségével. Az \(\displaystyle AC\) átló hosszát jelölje \(\displaystyle e\). Az \(\displaystyle ECD\) derékszögű háromszögben \(\displaystyle \cos30^{\circ}=\frac{e/2}{x}\), amiből \(\displaystyle e=x\sqrt3\).
Az \(\displaystyle EBC\) derékszögű háromszögből \(\displaystyle \cos50^{\circ}=\frac{e/2}{y}\), és így \(\displaystyle y=\frac{x\sqrt3}{2\cos50^{\circ}}\).
\(\displaystyle t_{ACD}=\frac12x^2\sin120^{\circ}=\frac{\sqrt3}{4}x^2.\)
\(\displaystyle t_{ABC}=\frac12ey\sin50^{\circ}=\frac12x\sqrt3\cdot\frac{x\sqrt3}{2\cos50^{\circ}}\sin50^{\circ}=\frac34x^2\rm{tg}50^{\circ}.\)
Tehát \(\displaystyle 900=x^2\left(\frac{\sqrt3}{4}+\frac34\rm{tg}50^{\circ}\right)\), amiből
\(\displaystyle x=\sqrt{\frac{900}{\frac{\sqrt3}{4}+\frac34\rm{tg}50^{\circ}}}\approx26,0444.\)
Ebből \(\displaystyle y\approx35,0895\) és \(\displaystyle k=2x+2y\approx122,2678\). Tehát körülbelül 122,27 méter hosszú kerítés szükséges a telek bekerítéséhez.
Statistics:
188 students sent a solution. 5 points: 120 students. 4 points: 11 students. 3 points: 33 students. 2 points: 4 students. 1 point: 16 students. 0 point: 4 students.
Problems in Mathematics of KöMaL, February 2013
