 Problem C. 1171. (May 2013)
Problem C. 1171. (May 2013)
C. 1171. One diagonal of a trapezium is 7 cm long. It divides the other diagonal into pieces of lengths 4.5 cm and 6 cm. The length of the shorter leg of the trapezium is 5 cm. Find the area of the trapezium.
(5 pont)
Deadline expired on June 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Mivel \(\displaystyle AB||DC\) és \(\displaystyle AE\), \(\displaystyle EC\), illetve \(\displaystyle BE\), \(\displaystyle ED\) pedig egy egyenesre illeszkednek, azért \(\displaystyle ABE_{\triangle}\sim CDE_{\triangle}\), és így \(\displaystyle \frac{BE}{ED}=\frac{4,5}{6}\), amiből \(\displaystyle BE=7-ED\) felhasználásával \(\displaystyle BE=3\) és \(\displaystyle ED=4\) következik.
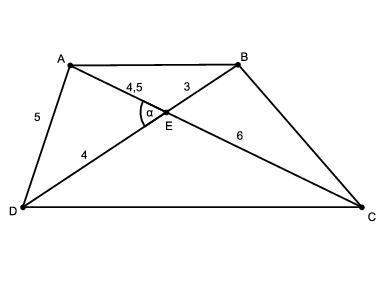
Írjuk fel a koszinusztételt az \(\displaystyle AED\) és a \(\displaystyle BEC\) háromszögre:
\(\displaystyle AD^2=4,5^2+4^2-2\cdot4,5\cdot4\cdot\cos\alpha,~~BC^2=3^2+6^2-2\cdot3\cdot6\cdot\cos\alpha;\)
\(\displaystyle AD^2=36,25-36\cos\alpha,~~BC^2=45-36\cos\alpha.\)
Ebből következik, hogy \(\displaystyle AD<BC\), ahonnan \(\displaystyle AD=5\). Vagyis \(\displaystyle 5^2=36,25-36\cos\alpha\), amiből \(\displaystyle \cos\alpha=0,3125\). Mivel \(\displaystyle 0<\alpha<180^{\circ}\), így \(\displaystyle \sin\alpha=\sqrt{1-0,3125^2}\).
A trapéz területe:
\(\displaystyle T=\frac{AC\cdot BD\cdot\sin\alpha}{2}=\frac{(4,5+6)\cdot7\cdot\sqrt{1-0,3125^2}}{2}\approx34,91 {\rm{~cm}}^2.\)
Statistics:
110 students sent a solution. 5 points: Bereczki Zoltán, Berta Dénes, Borbényi Márton, Büki Máté, Csikós Endre, Demeter Dániel, Fülep Andrea , Gnandt Balázs, Gyurcsik Dóra, Horeftos Leon, Kovács-Deák Máté, Köte Ákos, Németh Klára Anna, Radnai Bálint, Schrettner Bálint, Széles Katalin, Telek Máté László, Tóth Adrián, Tóth Zsófia, Vágó Ákos, Varga 149 Imre Károly, Varga Rudolf, Várkonyi Dorka, Williams Kada, Zsakó Ágnes, Zsiros Ádám. 4 points: 62 students. 3 points: 14 students. 2 points: 2 students. 0 point: 1 student. Unfair, not evaluated: 5 solutionss.
Problems in Mathematics of KöMaL, May 2013
