 Problem C. 1173. (May 2013)
Problem C. 1173. (May 2013)
C. 1173. Consider the line . Find the distance from the line to those points of integer coordinates that are the closest to the line but do not lie on the line.
(5 pont)
Deadline expired on June 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
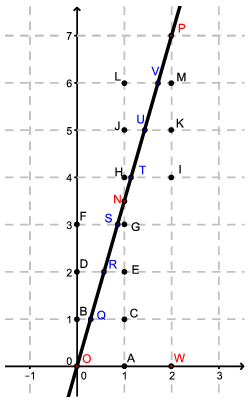
Megoldás. Tekintsük az ábrát. Látható, hogy elég az \(\displaystyle OP\) szakasz pontjait vizsgálni, hiszen az elhelyezkedés ismétlődik. Itt pedig elég a fekete pontoknak az egyenestől való távolságát vizsgálni. Mindegyik távolság egy derékszögű háromszög átfogóhoz tartozó magassága: az \(\displaystyle A\) ponté az \(\displaystyle OAN\), a \(\displaystyle B\) ponté a \(\displaystyle BCN\) stb., a \(\displaystyle H\) ponté a \(\displaystyle THN\), az \(\displaystyle I\) ponté a \(\displaystyle TIP\) stb., az \(\displaystyle M\) ponté a \(\displaystyle VMP\) háromszög magassága. Ezek a háromszögek mind hasonlók egymáshoz, hiszen derékszögűek, és egyik hegyeszögük is megegyezik, hiszen tangense mindegyik esetben \(\displaystyle 7/2\). Hasonló háromszögek közül annak a megfelelő magassága a legkisebb, amelyiknek a hosszabbik befogója a legkisebb a háromszögek közül. Ez a mi esetünkben az \(\displaystyle SGN\) és a \(\displaystyle THN\) háromszög, melyek hosszabbik befogója 1/2, vagyis az \(\displaystyle OWP\) háromszög befogójának 14-ede. Az \(\displaystyle OWP\) háromszög területének kétszerese: \(\displaystyle 2t=2\cdot7=\sqrt{2^2+7^2}\cdot m\), amiből \(\displaystyle m=\frac{14}{\sqrt{53}}\). A keresett távolság ennek a 14-ed része, vagyis \(\displaystyle \frac{1}{\sqrt{53}}\).
Statistics:
84 students sent a solution. 5 points: 52 students. 4 points: 15 students. 3 points: 7 students. 2 points: 5 students. 0 point: 5 students.
Problems in Mathematics of KöMaL, May 2013
