 Problem C. 1174. (May 2013)
Problem C. 1174. (May 2013)
C. 1174. The edges of a cube are coloured in three different colours such that parallel edges are the same colour. The points dividing the edges 1:2 are marked. Two marked points of each colour are selected at random. What is the probability that they are all coplanar? (It is not required to prove that the six points of a selection are coplanar.)
(5 pont)
Deadline expired on June 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Tekintsük a kocka egyik lapját, és vizsgáljuk meg, hogy milyen esetben kapunk megfelelő síkot. (Két pontot kiválasztva, az őket összekötő szakasz körül forgatva a síkot.) Legyen a kiválasztott lap az \(\displaystyle ADFG\) lap, amely zöld és kék éleket tartalmaz.
1.1 A lapról egy pontot sem választunk ki. Ekkor zöld és kék pontokat csak a \(\displaystyle BCEH\) lapról választhatunk, így - mivel onnan 4 pontot kell választani - a sík a \(\displaystyle BCEH\) sík lenne, ami azonban nem megfelelő.
1.2 A lapról 1 pontot választunk. Ekkor a \(\displaystyle BCEH\) síkról 3 pontot kell választani, ami az előző esethez hasonlóan nem lehetséges.
2.1 A lapról 3 vagy 4 pontot választva maga a lap lenne a sík, ami szintén nem jó.
3.1 A lapról 2 egyszínű pontot választunk. Az ezeket összekötő szakasz vagy átmegy a lap középpontján (pl. \(\displaystyle JK\)), vagy nem (pl. \(\displaystyle JL\)). De egyik esetben sem találunk megfelelő síkot.
3.2 A lapról 2 különböző színű pontot választunk. Ez háromféleképpen történhet: a \(\displaystyle JQ\), a \(\displaystyle JR\), illetve az \(\displaystyle IR\) szakaszokhoz hasonlóan. Az első és a harmadik esetben találunk egy megfelelő síkot, a második esetben nincs ilyen sík.
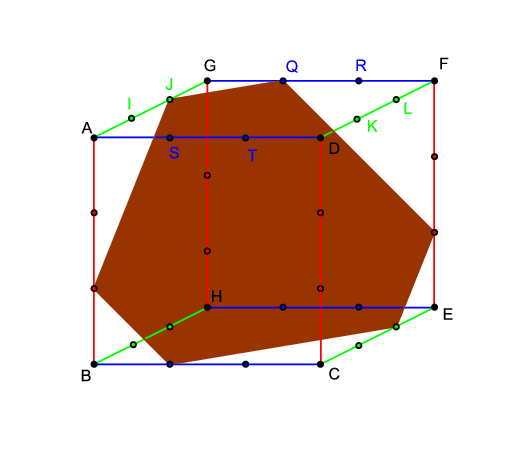
A két sík által a kockából lemetszett síkidom egybevágó: minden lapon vagy egy \(\displaystyle JQ\) típusú (két szomszédos él közös csúcsához közelebbi harmadolópontjait összekötő), vagy egy \(\displaystyle IR\) típusú (két szomszédos él közös csúcsától távolabbi harmadolópontjait összekötő) él van. Tekintsük ismét az \(\displaystyle ADFG\) lapot. Az erről a lapról kiválasztott él a következő 8 él valamelyike lehet: \(\displaystyle JQ\), \(\displaystyle IR\), \(\displaystyle RL\), \(\displaystyle QK\), \(\displaystyle IS\), \(\displaystyle JT\), \(\displaystyle TK\) vagy \(\displaystyle SL\). Tehát 8 megfelelő sík van.
Az összes lehetőség a 6 pont kiválasztására pedig \(\displaystyle \binom82^3\), hiszen mindhárom színből 8 pont van, amiből kettőt választunk ki.
A keresett valószínűség: \(\displaystyle \frac{8}{\binom82^3}=\frac{8}{28^3}=\frac{1}{14^3}\approx3,64\cdot10^{-4}\).
Statistics:
58 students sent a solution. 5 points: Bereczki Zoltán, Borbényi Márton, Demeter Dániel, Farkas Dóra, Fehér Zsuzsanna, Fekete Panna, Fülep Andrea , Holczer András, Horváth 016 Gábor, Kosztolányi Kata, Lajkó Kálmán, Máté Bálint, Molnár-Sáska Zoltán, Németh Klára Anna, Széles Katalin, Sziegl Benedek, Temesvári Fanni, Tóth Adrián, Trinyik Flóra, Varga 149 Imre Károly, Varga Rudolf, Zsakó Ágnes. 4 points: Andó Angelika, Gnandt Balázs, Lengyel Ádám, Pammer Tamás, Radnai Bálint, Szendrei Judit, Szilágyi Krisztina, Williams Kada. 3 points: 14 students. 2 points: 6 students. 1 point: 7 students. 0 point: 1 student.
Problems in Mathematics of KöMaL, May 2013
