 Problem C. 1180. (September 2013)
Problem C. 1180. (September 2013)
C. 1180. Investigate which of the squares inscribed in an acute-angled triangle has maximum side.
Suggested by R. Gyimesi
(5 pont)
Deadline expired on October 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Először határozzuk meg a háromszög \(\displaystyle a\) oldalára illesztett négyzet oldalának hosszát. Az \(\displaystyle AKI\) és az \(\displaystyle ABC\) háromszögek szögei egyenlők, ezért hasonlóak, és így \(\displaystyle \frac xa=\frac{m_a-x}{m_a}\), amiből \(\displaystyle x=\frac{am_a}{a+m_a}\).
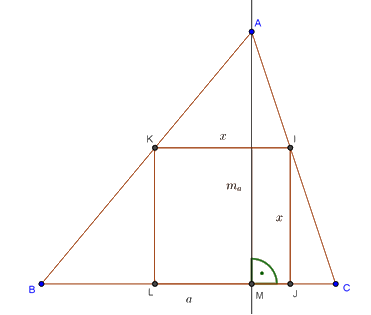
Tekintsük például az \(\displaystyle a<b\) esetet. Azt kell eldöntenünk, hogy az \(\displaystyle \frac{am_a}{a+m_a}\) és a \(\displaystyle \frac{bm_b}{b+m_b}\) hosszúságú szakaszok melyike a nagyobb. Mivel \(\displaystyle am_a=2t=bm_b\), ahol \(\displaystyle t\) az \(\displaystyle ABC\) háromszög területét jelöli, ezért elegendő a törtek nevezőjét összehasonlítanunk. Ennek érdekében tekintsük a két nevező eltérését:
\(\displaystyle a+m_a-(b+m_b)=a-b+\frac{2t}{a}-\frac{2t}{b}=(a-b)\left(1-\frac{2t}{ab}\right)\leq0,\)
hiszen a szorzat első tényezője negatív, a második pedig nem negatív (\(\displaystyle m_a\leq b\) miatt ugyanis \(\displaystyle 2t=am_a\leq ab\)). (Egyenlőség csak \(\displaystyle a\perp b\) esetén teljesülhet.)
Arra jutottunk tehát, hogy \(\displaystyle a<b\) esetén az \(\displaystyle a+m_a\) összeg nem lehet nagyobb a \(\displaystyle b+m_b\) összegnél, ebből kifolyólag az \(\displaystyle a\) oldalon "nyugvó" négyzet oldala legalább akkora, mint a \(\displaystyle b\) oldalra "támaszkodóé".
Statistics:
47 students sent a solution. 5 points: Bereczki Zoltán, Farkas Dóra, Hegel Patrik, Horváth Bendegúz, Kovács 972 Márton, Orbán Szandra, Sziegl Benedek, Tóth Zsófia. 4 points: Barna Kinga, Meleg András, Németh Klára Anna, Pammer Tamás, Temesvári Fanni, Tomai Fanni. 3 points: 4 students. 2 points: 6 students. 1 point: 6 students. 0 point: 17 students.
Problems in Mathematics of KöMaL, September 2013
