 Problem C. 1183. (October 2013)
Problem C. 1183. (October 2013)
C. 1183. The lattice points lying on the circle of radius 5 about the origin of the coordinate plane determine a convex polygon. What is the area of this polygon?
(5 pont)
Deadline expired on November 11, 2013.
Sorry, the solution is available only in Hungarian. Google translation
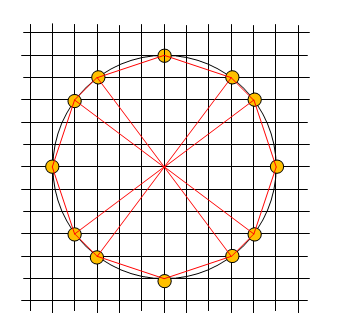
Megoldás. Az origó középpontú, 5 egység sugarú körre 12 rácspont illeszkedik, a (0;5), (5;0), (0;-5) és a (-5;0), illetve azok, melyek egy olyan derékszögű háromszög csúcsai, melynek az átfogója 5. Ilyen háromszög csak egy van, a 3, 4 és 5 egység oldalú. Az ennek megfelelő pontok a (3;4), (4;3), (3;-4), (4;-3), (-3;-4), (-4;-3), (-4;3) és a (-3;4) koordinátájú pontok.
Az így kapott tizenkétszöget 8 részre osztjuk, 4 egybevágó deltoidra, és 4 háromszögre.
A deltoidok területe egyenként \(\displaystyle \frac{5\cdot6}{2}=15\), tehát összesen \(\displaystyle 4\cdot15=60\).
A háromszögek alapja \(\displaystyle \sqrt2\), magassága \(\displaystyle 4\sqrt2-0,5\sqrt2=3,5\sqrt2\), így egy háromszög területe \(\displaystyle \frac{\sqrt2\cdot3,5\sqrt2}{2}=3,5,\) tehát összesen \(\displaystyle 4\cdot3,5=14\).
A tizenkétszög területe így \(\displaystyle 60+14=74\) egység.
Bekő Zsófia 10. o. t., Mosonmagyaróvári Kossuth Lajos Gimnázium
Megjegyzés: Egy háromszög területét megkaphatjuk másképp is, például úgy, hogy a köré írható \(\displaystyle 4\times4\)-es négyzet területéből kivonjuk három derékszögű háromszög területét.
Statistics:
214 students sent a solution. 5 points: 109 students. 4 points: 56 students. 3 points: 17 students. 2 points: 8 students. 1 point: 9 students. 0 point: 13 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, October 2013
