 Problem C. 1187. (October 2013)
Problem C. 1187. (October 2013)
C. 1187. The shorter diagonal cuts a parallelogram into two triangles. Consider the inscribed circle of one triangle, and the escribed circle of the other triangle that touches the diagonal. Prove that the four points of tangency not lying on the diagonal are collinear.
(5 pont)
Deadline expired on November 11, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásvázlat. Betűzzük a paralelogramma csúcsait és a két kör érintési pontait az ábra szerint. Legyen AB=CD=c, BC=DA=b és BD=a, és legyen s=(a+b+c)/2.
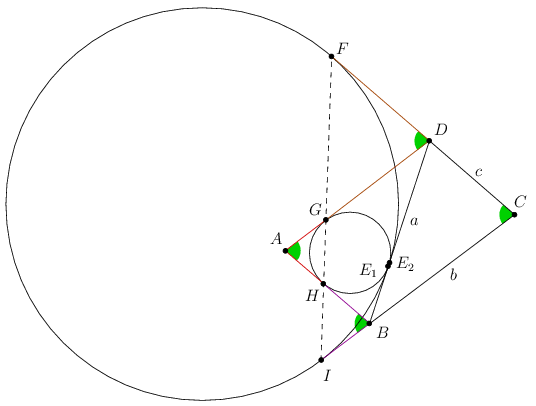
Az ABD háromszög oldalainak hossza a, b és c, tehát a csúcsok és a beírt kör érintési pontja közötti távolságok: AG=AH=s-a, BH=BE1=s-b és DG=DE1=s-c.
A CDB háromszög oldalainak hossza is a, b és c. A csúcsok és a BD oldalhoz hozzáírt kör érintési pontjai közötti távolságok: CF=CI=s, BI=BE2=s-b és DF=DE2=s-c.
Az AHG, BHI és DFG háromszögek egyenlő szárúak: AH=AG=s-a, BH=BI=s-b és DF=DG=s-c. Továbbá a három háromszög szárszöge ugyanakkora. Az AHG, BHI és DFG háromszögek tehát hasonlók. Ezért AHG =BHI
=BHI , vagyis I a GH egyenesre esik; és ugyanígy HGA
, vagyis I a GH egyenesre esik; és ugyanígy HGA =FGD
=FGD , tehát F is a GH egyenesre esik.
, tehát F is a GH egyenesre esik.
Megjegyzés. Mivel BE1=BE2, a két kör ugyanabban a pontban érinti a BD szakaszt.
Statistics:
32 students sent a solution. 5 points: Bekő Mária, Bereczki Zoltán, Chourfi Abdel Karim, Denke Dorottya, Farkas Dóra, Németh Klára Anna, Porupsánszki István, Szabó 157 Dániel, Szabó 524 Tímea, Sziegl Benedek, Szőke Tamás, Zsiros Ádám. 4 points: Gnandt Balázs, Hegel Patrik, Temesvári Fanni. 3 points: 6 students. 2 points: 7 students. 1 point: 3 students. 0 point: 1 student.
Problems in Mathematics of KöMaL, October 2013
