A C. 1190. feladat (2013. november)

C. 1190. Bizonyítsuk be, hogy ha egy trapéz húrnégyszög és érintőnégyszög is egyben, valamint átlói merőlegesek egymásra, akkor csak négyzet lehet.

(5 pont)

A beküldési határidő 2013. december 10-én LEJÁRT.

I. megoldás. Ha egy trapéz húrnégyszög, vagyis húrtrapéz, akkor a szárai egyenlő hosszúak. Ha érintőnégyszög, akkor szemközti oldalainak összege egyenlő.

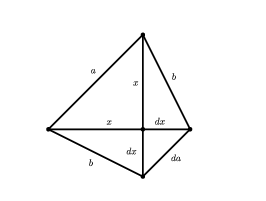
Mivel a húrtrapéz átlói két hasonló háromszöget határoznak meg, valamint szimmetrikus az alapok felezőmerőlegesére, ezért beírhatók az ábrába a szakaszok fenti hosszai. Írjunk fel egy-egy Pitagorasz tételt az \(\displaystyle a\), illetve a \(\displaystyle b\) átfogójú derékszögű háromszögekre: \(\displaystyle x^2+x^2=a^2\), \(\displaystyle x^2+(dx)^2=b^2\). Ezekből \(\displaystyle a=\sqrt2x\), \(\displaystyle b=\sqrt{x^2+d^2x^2}\) és \(\displaystyle da=d\sqrt 2x\).

Az érintőnégyszög szemközti oldalainak összege egyenlő:

\(\displaystyle \sqrt2x+d\sqrt2x=2\sqrt{x^2+d^2x^2}.\)

Ezt négyzetre emelve és rendezve:

\(\displaystyle 2x^2+2d^2x^2+4dx^2=4x^2+4d^2x^2,\)

\(\displaystyle 0=2x^2+2d^2x^2-4dx^2=2x^2(1+d^2-2d)=2x^2(d-1)^2.\)

Mivel \(\displaystyle x>0\), ezért ez csak \(\displaystyle d=1\) esetén lehetséges.

Ha pedig egy négyszög átlói merőlegesek, egyenlő hosszúak és felezik egymást, akkor a négyszög négyzet.

II. megoldás.

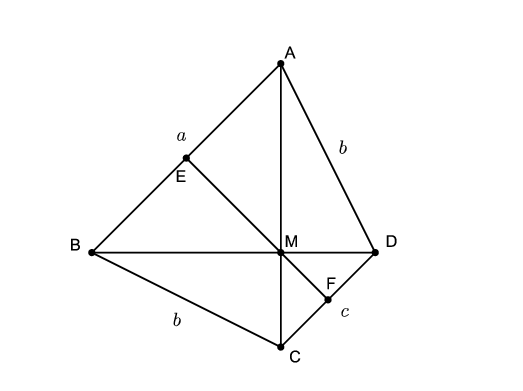
A húrnégyszög szárai egyenlő hosszúak, jelölje mindkettőt \(\displaystyle b\). Az érintőnégyszög szemközti oldalainak összeg egyenlő: \(\displaystyle a+c=2b\), amiből \(\displaystyle b=\frac{a+c}{2}\).

A húrnégyszög tengelyesen szimmetrikus, a szimmetriatengelye \(\displaystyle EF\), ahol \(\displaystyle E\) az \(\displaystyle AB\), \(\displaystyle F\) pedig a \(\displaystyle CD\) oldal felezőpontja. A szimmetria miatt az átlók \(\displaystyle M\) metszéspontja rajta van \(\displaystyle EF\)-en. Mivel az átlók merőlegesek egymásra, így \(\displaystyle BMA\angle=DMC\angle=90^{\circ}\). A Thalész tétel megfordítása szerint ekkor \(\displaystyle ME=\frac{AB}{2}=\frac a2\) és \(\displaystyle MF=\frac{CD}{2}=\frac c2\), így \(\displaystyle EF=ME+MF=\frac a2+\frac c2=b\).

Tehát a trapéz magassága ugyanolyan hosszú, mint a szára, így a trapéz téglalap, vagyis \(\displaystyle a=c\) is teljesül. Így \(\displaystyle b=\frac{a+a}{2}=a\), vagyis \(\displaystyle ABCD\) négyzet.

Statisztika:

130 dolgozat érkezett.
5 pontot kapott:	59 versenyző.
4 pontot kapott:	9 versenyző.
3 pontot kapott:	16 versenyző.
2 pontot kapott:	10 versenyző.
1 pontot kapott:	10 versenyző.
0 pontot kapott:	14 versenyző.
Nem versenyszerű:	12 dolgozat.

A KöMaL 2013. novemberi matematika feladatai